Énergie Nucléaire

Notations utilisées dans le chapitre:

Les indices suivants indiquent : n = neutrons, p = proton, e = électron.
N_n = nombre de neutrons dans l'élément X
X = symbole de l'atome (U pour uranium par exemple)
m_n = masse du neutron, m_Xobs = masse mesurée de l'atome

Sommaire de la page

I) L'atome

I.1) Constitution de l'atome
I.2) Constitution du noyau
I.3) Caractéristiques de l'atome
I.4) Isotopes de l'atome
I.5) Energie de l'atome
I.6) Excitation de l'atome
I.7) Les particules α
I.8) Les particules β
I.9) Les particules γ

II) Probabilités de réaction de l'atome

II.1) Probabilité d'émission d'une particule
II.2)Activité
II.3)Production de neutrons

III) Interaction des neutrons avec la matière

III.1) Les deux types d'interactions possibles
III.2) La réaction en chaîne
III.3) Ralentissement des neutrons rapides
III.4) Puissance pouvant être extraite de l'uranium
III.5) Contrôle de la réaction
III.6) Types de réacteurs, principes technologiques

IV) Taille critique du réacteur

IV.1)Puissance dégagée par la fission
IV.2)Bilan neutronique
IV.3)Détermination de l'absorption

V) Transfert de puissance

V.1)Limites thermiques de l'échange de chaleur
V.2)Système à deux cycles
V.3)Le réacteur CANDU

VI) Les échangeurs de chaleur

VI.1)Rappels de thermique et présentation du problème
VI.2)Conduction dans un cylindre plein
VI.3)Conduction dans un cylindre creux
VI.4)Convection forcée

VI.4.1)Calcul des températures
VI.4.2)Mélange diphasique
VI.4.3)Assèchement
VI.4.4) Caléfaction

---

Avant-propos

La fission nucléaire à été découverte en Suisse en 1939. C'est Einstein qui en a permis la compréhension. Nucléaire fait référence au noyau de l'atome.

La fission nucléaire nécessite un combustible fossile, l'Uranium 235 (₉₂U²³⁵), 238 (₉₂U²³⁸), ou le Thaurium (₉₀U²³²). Seuls ces trois peuvent être utilisés pour la fission nucléaire.

La combustion de l'uranium permet d'obtenir de l'énergie et un résidu qui s'avère être un combustible encore meilleur. La densité d'énergie de l'uranium est très grande (1kg =>1400 tonne de charbon). On estime qu'il y à 10¹²t d'uranium 235 sur terre (c'est à dire beaucoup).

Avec les machines thermiques, on reste en surface de l'atome, on ne touche qu'aux électrons. Alors qu'avec le nucléaire, on va chercher l'énergie dans le noyau de l'atome.

L'atome

Constitution de l'atome

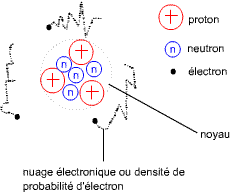
Un atome est formé par un gros noyau (formé par des protons et des neutrons) et de très petites particules (les électrons) s'agitant à proximité de ce noyau.
Un atome est formé de particules élémentaires (encore inconnues, mais que l'on à mesurées):

- Des protons, charges électriques regroupées ensemble dans un très petit espace. Leur charge électrique est par convention positive.

- Des électrons, ayant une orbitale autour du noyau, et de charge électrique négative. On ne peut savoir à la fois où et quand on les trouvera.

- Des neutrons, de charge électrique neutre, ayant pour fonction de coller les protons entre eux.

Les deux constituants du noyau, les neutrons et les protons, sont appelés les nucléons.

Constitution du noyau

Les protons étant des charges électriques positives, il s'exerce alors sur eux (voir le cours d'électricité) une force tendant à les éloigner l'un de l'autre. Il s'agit de la force coulombienne.

Cette force est proportionnelle à l'inverse du carré de la distance séparant les deux charges. Plus la distance se réduit, plus la force coulombienne devient forte, au carré de la distance.

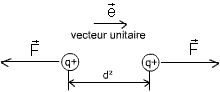
Or, les protons dans le noyau sont très proches, et ils devraient être repoussés entre eux. Ce sont les neutrons qui assurent la cohésion du noyau, en générant la force nucléaire (attirant deux charges électriques de même signe). C'est un échange de nucléons qui maintiennent ensemble les neutrons et les protons. Cette force nucléaire est très importante, mais à une distance d'application très faible comparée à la force coulombienne.

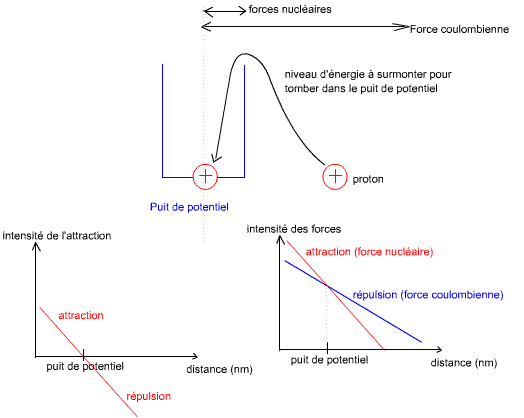
L'énergie contenue dans le coeur des atomes, et qui sert à la cohésion du noyau (contrant les forces coulombienne) est celle de l'origine de l'univers, lorsque l'atome à été créé (c'est l'énergie qu'il a fallu pour coller les protons entre eux, donc l'énergie dépensée pour créer les atomes).

Pour passer le puit de potentiel, il y a plusieurs méthodes:

- Créations de mions (particules négatives aussi massives qu'un proton) => demande beaucoup d'énergie.
- Soit par application d'une énorme pression (par exemple, la pression d'un laser sur une bille de verre). La pression rapproche les deux particules de même signe jusqu'a ce que la distance soit inférieure à la distance du puit de potentiel, et là ce sont les forces nucléaires (d'attraction) qui entrent en jeu.

Caractéristiques de l'atome

La mesure est arbitraire, car c'est une invention de l'homme. On compare deux choses semblables. Les masses sont comparées à la mesure étalon conservée à Paris.

Les masses:
électron : 9,1093897.10^-31 kg (au repos) = 5,486.10^-4 uma
proton : 1,673.10^-27 kg = 1,007276 uma
neutron :1,675.10^-27 kg = 1,008665 uma

Les charges électriques :
électron: - 1,6027733.10^-19 C (Coulomb)
proton: 1,6027733.10^-19 C
neutron: 0 C

Représentation dans la classification de Mendeleïev: _ZX^A avec X le symbole de l'atome (ex: "U" pour l'uranium), Z le nombre de protons et donc d'électrons pour l'équilibre électrique, et A la masse atomique, exprimée en uma. Comme les masses des protons et neutrons sont très proches l'une de l'autre, et valent pratiquement 1 uma chacune, on fait la simplification suivante:
A = nombre de protons + nombre de neutrons, et
A-Z est le nombre de neutrons.

1 uma = 1 unité de masse atomique = 1/12 de la masse atomique du carbone 12 = 1,6604.10^-27 kg (c'est une unité arbitraire comme l'est le nombre d'Avogadro). On a choisi cette unité de masse car elle correspond grosso-modo à la masse d'un atome d'hydrogène H. Il est plus facile de mesurer à partir de l'atome de carbone (valant 12 uma) que de celui de l'hydrogène.

Isotopes de l'atome

Même si un atome est neutre du point de vue électrique (autant de protons que d'électrons) il peut se faire qu'au niveau quantique (nombre d'électrons par couche d'énergie) qu'un atome ne sera équilibré qu'avec un ou plusieurs électrons en plus ou en moins.

On est alors dans le domaine de la chimie. Une différence protons-électrons change alors complètement le comportement chimique de l'atome (il réagira avec d'autres produits pour donner ou prendre des électrons, notion de couple électrochimique: Cl^- est plus stable que Cl, ce dernier étant plus agressif envers son milieu environnant pour capturer un électron).

Si ce sont des neutrons que l'on ajoute, le comportement chimique de l'atome est inchangé. Mais il change au niveau nucléaire (le neutron n'a pas de charge mais à une masse). Il s'agit alors d'un isotope (différence dans le nombre de neutrons / à l'atome de la nomenclature).

Pour l'eau, on a l'exemple de l'atome d'hydrogène ₁H¹ (soit un proton et un électron) qui devient ₁H² (1 proton, 1 électron plus 1 neutron qui à été absorbé) lorsqu'il accepte un neutron supplémentaire. C'est un isotope de l'hydrogène, que l'on nomme Deutérium. Il s'agit de l'eau lourde. Cet isotope est présent naturellement dans l'eau, en faibles quantités.

Isotopes de l'uranium naturel:

- 0.0058% de ₉₂U²³⁴
- 0.72% de ₉₂U²³⁵ (c'est le combustible utile de l'uranium)
- 99,27% de ₉₂U²³⁸

Énergie de l'atome

La masse de l'atome est inférieure à la somme des masses des particules le constituant. Cette différence de masse s'explique par l'énergie libérée au moment de la création de l'atome. Cette énergie n'est plus récupérable par la suite, elle n'est pas contenue quelque part dans l'atome. Quand on fait une fusion ou une fission, on obtient des produits qui ont un plus grand défaut massique que le produit initial. Ce qui explique que les deux réaction libèrent de l'énergie sous forme de chaleur.

Soit m_X la masse mesurée (réelle) de l'atome, et m_Xthéo sa masse théorique (la somme des masses de ses constituants):

m_Xthéo = m_n ΣN_n + m_p ΣN_p + m_e ΣN_e > m_Xobs

avec m_p la masse d'un proton et N_p le nombre de protons présents dans l'atome.

Soit Δm la différence de masse (en uma) entre la masse théorique et celle observée, toujours plus faible . Cette différence provient du fait qu'une partie de la masse des constituants s'est transformée en énergie lors de la création de l'atome, énergie nécessaire pour combattre la force coulombienne entre les protons.

Δm = [ m_n (A-Z) + Z(m_p + m_e) ] - m_Xobs

D'après la relation d'Einstein, on trouve l'énergie qui a été prise pour fabriquer l'atome:

ΔE = Δm c²

avec c la célérité de la lumière (3.10⁸ m/s), et Δm exprimée en kg, donc multiplier la Δm précédemment trouvée en uma par 1,6604.10^-27 kg/uma. On peut donc en déduire l'énergie dissipée lors de la création de l'atome (qui n'est plus contenue dans l'atome).

Si l'on écrit l'équation de Einstein en se servant du fait que (m_p + m_e) = m_Xobs de l'hydrogène naturel ₁H¹, c'est à dire que la masse observée de l'hydrogène est la même que sa masse théorique (il n'y a qu'un seul proton, donc pas de force coulombienne à vaincre, donc pas d'énergie transformée lors de la création de l'atome d'hydrogène), on obtient:

ΔE = Δm c² = c² [Z*₁H¹+ (A-Z) m_n- m_Xobs]

C'est l'équation du défaut massique. ΔE est l'énergie manquante de l'atome, prise à la masse des particules lors de la création de l'atome. Cette équation a été vérifiée expérimentalement pour tous les éléments trouvés dans la nature. A noter que m_Xobs est fonction de A et de Z.

Transformation des Joules en MeV, plus pratique en nucléaire car l'unité convient bien aux calculs atomes par atomes:
Soit 1 V = 1 Joule/Coulomb. Et 1 électron = 1e = 1,6.10^-19 C.
Donc 1e.1V = 1 eV (électron-Volt) = 1,6.10^-19 (J / eV).
Pour passer des eV aux Joules, on fait l'opération suivante (les eV se simplifient) : x (eV) * 1,6.10^-19 (J / eV) = y (J)
Pour passer des Joules aux eV, on multiplie les Joules par 1 / 1.6.10^-19(J / eV) soit 6.25.10¹⁸ (eV / J).

Ex: Pour le Deutérium, ₁H² , la m_Xthéo = 2,106490 uma, et la m_Xobs = 2,014102 uma, soit une Δm = 0,002388 uma.
Energie contenue dans l'atome: ΔE = 0,002388 uma * 1,6604.10^-27 kg/uma * 3.10⁸ m²/s² = 0,0357.10^-11 Joules.
Cela fait beaucoup d'énergie pour un seul atome. Or, il y a vraiment beaucoup d'atomes dans un kg d'uranium.
Si on passe en MeV, on obtient: ΔE(₁H² ) = 0,0357.10^-11 (J) * 1/1,6.10^-19 (J/eV) = 2,2 MeV.

Si nous traçons le graphe de l'équation du défaut massique:

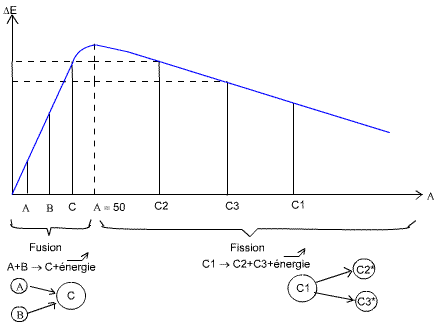
La fission consiste à séparer des atomes lourds, et la fusion à regrouper des atomes légers. A la fois la fission et la fusion produisent de l'énergie, due aux pentes inversées de chacune des réaction, faisant que les produits finaux possèdent toujours un ΔE supérieur aux produits de départ.
Les * indiquent que l'atome est dans un état excité (possède un neutron en trop).
On peut tout de suite remarquer que la fusion (réaction se passant dans le soleil) est plus énergétique que la fission: ΔE_fu>ΔE_fi.

Ex: Pour la fusion du deutérium ₁H² (de masse observée 2,0147 uma) et du tritium ₁H³ (2 neutrons dans le noyau, de masse observée 3,0169 uma).
₁H² + ₁H³ →₂He⁴ + n + énergie dégagée ΔE
avec n un neutron, émis lors de la fusion (envoyé à haute vitesse dans le milieu environnant). La masse observée de l'isotope d'hélium ₂He⁴ est de 4,0039 uma.
ΔE = c² [(m_{réactifs initiaux}) - (m_{produits finaux})] = c² [(m₁H² + m₁H³) - (m₂He⁴ +m_n)] = 3.10⁸ m²/s² [ (2,0147 + 3,0169) - (4,0039 + 1,0087)] * 1,6604.10^-27 kg/uma = 17,7 MeV.

Pour une fusion ou une fission, Δm est donc la différence de masse observée entre les réactifs de départ et la masse observée des produits de la réaction (plus faible). Cette différence de masse correspondant à l'énergie émise (sous forme de chaleur principalement) lors de la réaction.

Excitation de l'atome

Quand un atome est frappé par un neutron, il devient excité, c'est à dire qu'il contient trop d'énergie. Il va s'en libérer soit en émettant un rayonnement α, β ou γ, soit en réalisant une fission.

Si l'isotope contient trop de neutrons par rapport aux protons, l'atome devient instable (il est dit excité, on le repère par *).
Quand le nombre de neutrons est pair, l'atome est stable.
Si ce nombre est impair, l'atome possède alors un excès d'énergie et va tendre vers une énergie plus faible. On dit alors que l'atome est excité. L'excédent d'énergie va être libéré graduellement et lentement. Il dégage son excédent d'énergie en émettant des particules:

- les particules α : atomes d'hélium ₂He⁴ (cas du soleil). Ces émissions de gaz (2p+2n) s'arrêtent avec un sac plastique.
- les particules β : ce sont des électrons émis lors de la transformation d'un neutron en proton (n → p + e). S'arrêtent avec du papier.
- les particules γ : sous forme de photons (énergie électromagnétique) à la fréquence de 95,1.10¹² Hz. Ce sont les plus dangereuses, émises par les déchets radioactifs. Nécessite de grosses épaisseur de plomb ou de béton pour les arrêter.

Voyons ci-dessus le graphe périodique qui va nous aider à comprendre la diminution de l'énergie d'un atome excité :

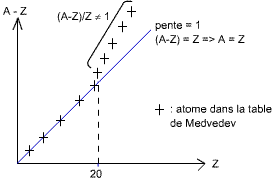
Fig. 4 : Graphe périodique

Il faut bien se rappeler que A-Z veut dire nombre de neutrons, A étant le nombre total de neutrons et de protons, et Z étant le nombre de protons donc d'électrons si la neutralité électrique est respectée.
Dans la classification périodique, jusqu'aux atomes ayant moins de 20 électrons, on trouve une égalité entre le nombre de neutrons et le nombre de protons. Ensuite, on s'aperçoit qu'il y a un excès de neutrons, ce qui signifie que les atomes sont excités et auront tendances à diminuer leur énergie en surplus par émission d'une particule α, β ou γ.

Les particules α

Les émissions α correspondent à l'émission par l'atome de 2 neutrons et de 2 protons, qui correspondent en faite au noyau d'Hélium (₂He⁴ = 2p + 2n). L'atome excité va donc diminuer son énergie en s'approchant des atomes plus légers (moins de protons et de neutrons), ces atomes étant plus stables.

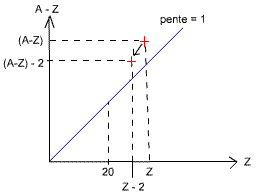
Le nombre de neutrons et de protons émis étant le même, l'atome reste au dessus de la pente de 1.
(A-Z) → (A-Z) - 2 et Z → Z - 2 (on enlève 2 neutrons à A-Z et on enlève 2 protons à Z).

Les particules β

L'atome excité impair, pour diminuer son énergie, peut aussi transformer un neutron en proton, afin d'équilibrer A-Z = 0. Il tend alors à redevenir pair donc stable (ligne de pente = 1).

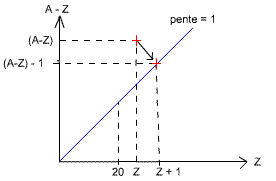
(n → p + e). => (A-Z) → (A-Z) - 1 => Z → Z + 1 (car l'électron issu de la réaction ne reste pas dans l'atome, seul un proton est rajouté à Z et un neutron enlevé à (A-Z)).
On passe d'une équation à l'autre en enlevant A de chaque côté de la première équation, ce qui ne marche pas pour les particules α, car on ne finit pas sur la pente =1 comme c'est le cas pour la particule β.

Les particules γ

Le photon émis à de très grandes longueurs d'ondes, de l'ordre des ondes radio.

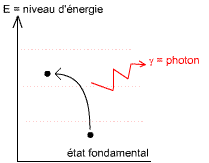
Les rayons γ sont générés différemment des rayons X. Ils pénètrent beaucoup plus profondément dans la matière (ex: on s'en sert pour le contrôle de soudures).
Les rayons X sont provoqués par un changement brutal d'énergie mécanique (ex: l'écran télé: les électrons sont accélérés puis arrêtés brutalement sur une plaque de cuivre, ce qui provoque l'émission des rayons X).

Les particules γ sont les plus dangereuses des trois, il faut une épaisse couche de plomb ou de béton pour les stopper. Ces particules ionisent la matière (création de charges électriques, donc modifient le fonctionnement cellulaire (c'est le fameux rayonnement ionisant)).

• Effets des particules γ sur la matière:

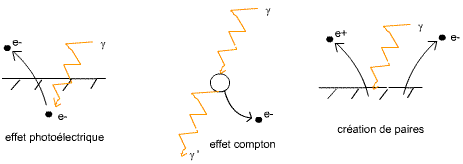
Avec e+ un positron, qui est une particule d'antimatière (pendant positif de l'électron).

• Protection contre les rayons γ:

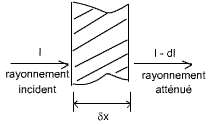dI= -μ I δx
avec μ (en m^-1, déterminé expérimentalement) le coefficient d'absorption des rayons γ, ce coeff étant très grand pour le plomb, l'eau ou le béton.
dI / I= -μ δx => I(x) = I₀ e^-μx
avec I0 constante fonction des conditions initiales.

 

 

II) Probabilités de réaction de l'atome

Probabilité d'émission d'une particule

Déterminons avec quelle probabilité l'atome excité va se débarrasser de son énergie excédentaire due à la présence de neutrons en trop.

Soit τ la constante de temps (en secondes), habituellement notée t. Soit N le nombre d'atomes de l'espèce considérée, et λ la constante de désintégration pour un atome (en nombre de désintégration par secondes, analogue à une fréquence).
Au fil du temps, les atomes vont se débarrasser de leur énergie, et se transformer en une autre espèce. N(τ) est le nombre d'atome de l'espèce considérée encore présent au temps τ (par exemple, pour τ = 50 ans), donc non encore transformés. Au début, il y a N₀ atomes excités.
On peut écrire:

dN / dτ = - λ N

dN / N = - λ dτ =>

Ce qui nous donne l'équation de base:

N(τ) = N₀ e^-λτ

Cette équation à la forme suivante:

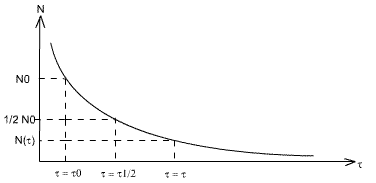
La demie vie de l'espèce est le temps au bout duquel la moitié de atomes du départ se seront transformés:

τ=τ_1/2 => N = N₀ / 2

τ_m est la période de désintégration: τ_m =1 / λ

Pour exprimer la demi vie en fonction de la période de désintégration :
N₀ / 2 = N₀ e^-λτ1/2 => ln N₀ - ln 2 = ln N₀ * (-λτ1/2 ) => τ_1/2 = 0,693 /λ
=> τ_1/2= 0,693 τ_m => λ= 0.693 / τ_1/2

Quelques exemples de demies vies d'éléments trouvés dans la nature, pour l'émission de particules α:

Uranium 235 (₉₂U²³⁵): τ_1/2 = 1,4.10¹⁰ années
Uranium 238 (₉₂U²³⁸): τ_1/2 = 4,5.10⁹ années
Thaurium (₉₀U²³²): τ_1/2 = 7,1.10⁸ années

On voit qu'il faut attendre longtemps avant que l'énergie se dégage par émission de particules α.

 

Activité

L'activité Act est le nombre de particules émises par secondes.

Act = -dN / dτ = λ N

L'activité se mesure en Curie (Ci): 1 Ci = 3,7.10¹⁰ (désintégrations par seconde)
On utilise aussi une autre unité, plus pratique, le Becquerel : 1 Bq = 1 désintégration/s (d/s).

On utilise ici l'atome-gramme plutôt que la mole.
L'atome-gramme est un ensemble d'atomes, de nombre d'atomes égal au nombre d'Avogadro. C'est donc une mole. La masse de l'atome-gramme est la masse atomique-gramme.
Soit A la masse atomique d'un atome, exprimée en grammes par atome-gramme, même valeur numérique que l'UMA (on prend donc la valeur de la masse atomique de l'atome dans la classification périodique pour A, soit _ZX^A ). C'est à dire que un atome-gramme de l'espèce X pèse A grammes.
Un atome-gramme pour une espèce est défini par le rapport du nombre d'Avogadro divisé par la masse atomique A de l'espèce : 1 atome-gramme = Na/A

N (nombre atomes) = [ Na (g/atome-gramme) * masse (g) ] / A

Soit Na le nombre d'Avogadro: Na = 6,023.10²³ atomes par atome-gramme.

Ci = λ (Na/A) = ( 0,693 * 6,023.10²³ ) / (3,7.10¹⁰ *A*τ_1/2 ) ???

Act (Ci) = 1,12.10¹³ / ( A*τ_1/2 ) désintégrations /s

Ex: Le corps humain contient une 250 g de potassium. 99,988% de cette masse est constituée de Knormal, et 0,012% de k⁴⁰ (émetteur de rayonnement β). La demie vie du potassium 40 est τ_1/2 (k⁴⁰) = 1,3.10⁹ années, et sa masse atomique Ak⁴⁰ = 40 g/atome-gramme.
La masse de k⁴⁰ = %k⁴⁰ * masse totale de K = 0,012 % * 250 g = (0,00012) * 250 = 0,03 g
Donc Mk⁴⁰ = 0,03 g de k⁴⁰ dans le corps humain.
Cela équivaut à Mk⁴⁰ / Ak⁴⁰ = 0,03 (g) / 40 (g/atome-gramme) = 7,5.10^-4 atome-gramme de potassium dans le corps humain.
Nombre d'atomes de k⁴⁰ contenu dans le corps: Nk⁴⁰ = (Mk⁴⁰ / Ak⁴⁰)*Na = 7,5.10^-4 * 6,023.10²³ = 4,5.10²⁰ atomes.
Constante de désintégration du k⁴⁰ : τ_1/2 (k⁴⁰) = 1,3.10⁹ = 0.693 / λ=> λ(k⁴⁰) = 5,3.10^{-10 (d/an)}
Activité du potassium 40: -dN(k⁴⁰)/ dτ= λN(k⁴⁰) = 5,3.10^-10 *4,5.10²⁰ = 2,4.10¹¹ (atomes/an) ou radiations β par années.
-dN(k⁴⁰)/ dτ= 2,4.10¹¹ / (365*24*3600) = 7 600 radiations b par secondes.

Production de neutrons

On peut générer des neutrons à partir des rayonnements α et γ.

A partir du rayonnement α

Pu²³⁹ émet un rayonnement α (₂He⁴) qui frappe du ₄Be⁹ ce qui donne un atome ₆X¹³*(atome X non défini dans la classification, à l'état excité*), diminuant son énergie en émettant un neutron, et en se transformant par là même en carbone 12 : ₆C¹² + 1 neutron.

A partir du rayonnement γ:

A* => perd de l'énergie en émettant un photon (rayonnement γ). Ce photon frappe le deutérium (D₂O) de l'eau lourde, qui devient excité. Il va perdre son énergie en émettant un neutron qui va frapper l'oxyde d'uranium :
(O₂U). g → ₁H² → ₁H²* → ₁H¹ + neutron

 

III) Interaction des neutrons avec la matière

Les deux types d'interactions possibles

Soit il y a dispersion, c'est à dire que les neutrons perdent progressivement de leur énergie au fur et à mesure de leurs nombreuses collisions avec les atomes.

Soit il y a absorption :

- Capture : le neutron rentre dans le noyau, celui-ci devient excité. Il fera décroitre son énergie excédentaire par un rayonnement >α, β ou γ.
- Fission : en frappant le noyau, le neutron va le séparer en deux.

La réaction en chaîne

Absorption:
Quand les neutrons sont rapides (énergie élevée), seul l'Uranium 238 peut les capturer (principe de superphénix en France). Ce neutron ne peut être utilisé pour faire la fission qui libérera l'énergie (dans superphénix, il ne produit qu'une capture => émission ultérieur de rayonnement).
Il faut ralentir les neutrons, ce qui est fait par dispersion dans l'eau. Au bout d'un moment ils deviennent lents, ils sont alors appelés neutrons thermiques. Ils peuvent alors être absorbés par l'uranium 235 et 238, cette absorption produisant soit un rayonnement, soit une fission (ce qui nous intéresse dans ce cas là).

Si il y a fission, on obtient alors:

• deux atomes A* et B* excités, dont la somme des masses observées est inférieure à la masse observée de l'uranium 235 de départ (donc énergie libérée)

• Une énergie libérée ΔE (environ 200 MeV par fission) provenant du défaut de masse.

• 2 neutrons rapides (que l'on ralenti puis que l'on réinjecte dans le cycle, ce qui nous donne la réaction en chaîne)

La probabilité de fission de l'U²³⁸ est très faible (c'est l'un des deux constituants de l'uranium naturel, avec l'U²³⁵, susceptibles de produire une fission).

Il y a des pertes de neutrons dans l'eau, car certains neutrons sont absorbés par l'eau durant la dispersion. Schéma résumant les interactions neutrons-matière et la réaction en chaîne:

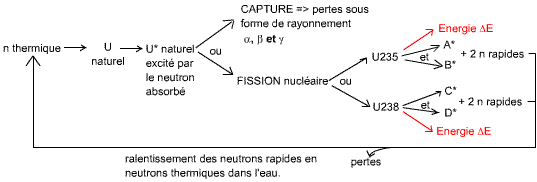
Quand le réacteur est critique, c'est que le nombre de neutrons injectés dans le réacteur (nombre de n initial) est égal au nombre de neutrons obtenus après réaction (nombre de n après fission) est le même.

Si nombre de n initial = nombre de n après fission => réacteur critique
Si nombre de n initial > nombre de n après fission => réacteur sous critique
Si nombre de n initial < nombre de n après fission => réacteur sur critique

Ralentissement des neutrons rapides

On ralentit les neutrons rapides par des chocs consécutifs semi-élastiques, afin d'augmenter la probabilité d'absorption. L'eau légère ralentit bien, par contre elle absorbe une partie des neutrons. En France,on utilise donc l'eau lourde comme modérateur, alors qu'au Canada, où l'uranium est moins cher (et où l'économie prime sur l'environnement) on utilise de l'eau légère. L'eau lourde absorbe moins les neutrons que l'eau légère, c'est pourquoi, à cause du nombre supérieur de neutrons frappant le combustible, il faut que celui-ci soit enrichi en U235 (France, Usa) ce qui coûte plus cher. Le meilleur système modérateur est le graphite (comme Tchernobyl).

Soit n(En) le nombre de neutrons à l'énergie En, et n₀ le nombre de neutrons total. Le graphique ci-dessous détermine le pourcentage de neutron possédant une énergie En (énergie du neutron).

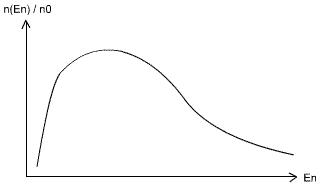
Avec k la constante de Boltzmann, k = 8,6.10^-5 (eV/K),
En = 1/2 m_n Vn², et m_n = 1,67.10^-27 kg (la masse du neutron).
La vitesse des neutrons Vn = 1,4.10⁶ √ En (m/s)

La vitesse du neutron ainsi que son énergie varie en fonction de la température:(vérifier les valeurs ci dessous avec les équations du dessus, il semblerait qu'il y ai des erreurs).

T (°C)	En (eV)	Vitesse (m/s)
20	0,025	2200
200	0,041	2800
400	0,058	3400
600	0,075	3800

Les neutrons lents verront une section efficace plus grande qu'un neutron rapide.

III.4) Puissance pouvant être extraite de l'uranium

Il faut être capable de déterminer la puissance thermique que l'on peut tirer d'un gramme d'uranium:

On introduit ici la notion de section efficace, qui est un concept probabiliste: C'est la surface que voit le neutron quand il va interagir avec un atome.
La section efficace est fonction de:

- du flux de neutrons Θ_n (en nombre de neutrons / cm².s) par unité de surface et de temps.
- de la vitesse des neutrons (neutrons rapide ou thermique).
- du type de noyau

Quand le neutron s'approche du noyau, s'il le voit gros, il à plus de chances de la frapper.

Prenons une plaque d'épaisseur δx, avec une densité N (nb d'atomes/cm³). Cette plaque est frappée par un flux de neutrons I (en nb neutrons / cm²). Voir la figure 19.

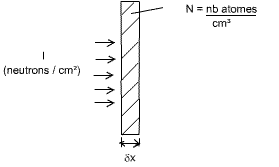
Fig. 19 : Plaque frappée par un flux de neutrons

On peut écrire que N.δx = nb d'atomes / cm².

Soit σ la section efficace: σ =
avec (nb neutrons / cm²) le flux de neutron incident, et c le nombre d'interaction par unité de surface.

σ = c / (N.δx.I)

On s'aperçoit que N.δx.σ = c/I << 1, faible probabilité, il faut donc envoyer un grand nombre de neutrons pour produire quelques interactions.

L'unité de σ est le cm² / noyau (surface efficace du noyau vu par le neutron). Le noyau de l'unité est équivalent au nombre d'atomes, car on assimile la surface de l'atome à celle de son noyau. Cette unité est très petite (entre 10^-22 et 10^-26). On utilise alors une autre unité, le Barn: 1 Barn = 10^-24 (cm²/atome).

Pour déterminer la taille de notre réacteur (masse critique) on introduit la notion de section efficace macroscopique Σ.

Σ= N.σ (1/cm)

C'est l'inverse d'une longueur, 1/Σ est la distance moyenne parcourue par un neutron avant d'être absorbé, ce qui nous donne une idée des dimensions du réacteur (pour le réacteur Candu, 1/Σ est de 12cm).

Soit ρ en g/cm³, A la masse atomique et Na le nombre d'avogadro.

N = Na. ρ / A donc Σ = (Na. ρ / A )σ

Pour une molécule (mélange) formée d'atomes différents:
Soit ν_i la fraction d'atomes du type i dans un mélange (ex: pour l'eau, ν_H = 2 car il y a 2 atomes d'hydrogènes dans une molécule d'eau H₂O), N_i le nombre d'atomes du type i et M la masse moléculaire du mélange (comme H₂O par exemple).

Σ_i = (Na. ρ / M )ν_i σ_i , et Σ_tot = Σ₁ + Σ₂+ ... + Σ_n

Σ_tot = (Na. ρ / M ) [ν₁ σ₁ + ν₂ σ₂ + ... + ν_n σ_n ]

Pour l'uranium naturel, les sections efficaces sont les suivantes:
U²³⁸ → σ_U238 = 2,71 Barn
U²³⁵ → σ_U235 = 683 Barn

Ex: Pour l'eau, ... voir dos au bas page 19)

voir la suite page 20.

Ce que nous pouvons retenir, c'est que la section efficace macroscopique est fonction de la densité. Plus celle ci est élevée, plus les atomes dans la plaque seront proches les uns des autres et plus le neutron sera absorbé rapidement (et plus Σ sera grand, donc plus grande section efficace, et 1/Σ, le chemin parcouru avant interaction, sera faible).

Contrôle de la réaction

Nous avons vu précédemment le chemin moyen parcouru par le neutron avant de produire une interaction avec un atome. Cette interaction produira soit un rayonnement (α, β et γ) soit une fission.
Voyons le nombre de neutrons participants réellement à la fission, en fonction des probabilités de pertes le long du circuit:

La fission de l'U²³⁵ et de l'U²³⁸ produisent une émission de neutrons rapides. La fission de l'U²³⁵ produit n neutrons, et comme la fission de l'U²³⁸ est bien plus rare(rayonnement favorisé), on note ε le pourcentage de neutrons produits par la fission de l'U²³⁸ par rapport aux n neutrons produits par l'U²³⁵, pourcentage auquel on rajoute 100% pour obtenir un facteur de multiplication de n. Comme ε est un facteur multiplicatif (1,00...), en multipliant n et ε on obtient le nombre total de neutrons émis.

Tout au long du cycle, les neutrons émis vont subir les quelques pertes ci-dessous:
Au niveau des neutrons rapides émis (indicés f pour fast), on a des pertes à cause des fuites (tous les neutrons ne se dirigent pas vers le réacteur, mais aussi vers les parois de béton et de plomb où ils sont absorbés. D'où l'idée de superphénix d'entourer le réacteur de produits de fission afin de récupérer utilement ces neutrons). Soit P_nlf la probabilité que les neutrons rapides ne fuient pas (non leak fast). La probabilité de pertes est donc de ( 1-P_nlf ).
Il y a par la suite toutes sortes de pertes pour les neutrons.
Lors de la dispersion, les neutrons rapides peuvent être absorbés par le système et par l'eau => pertes (1-p).
Une fois obtenus les neutrons lents, ils peuvent être émis ailleurs que vers le système, => pertes ( 1-P_nlth ). Si ils sont émis vers le système, ils peuvent être absorbés par les éléments de celui-ci autres que l'uranium 235 ou 238 => pertes ( 1-f ).
Une fois le neutron absorbé par l'uranium 235 ou 238, celui-ci peut perdre son énergie excédentaire apporté par le neutron en émettant un rayonnement => pertes (1-η).

La figure ci-dessous résume parfaitement le nombre de neutrons émis initialement et ceux que l'on retrouve en sortie.

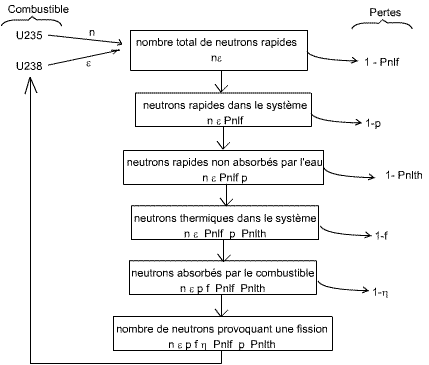
Avec:
nε le nombre total de neutrons émis par la fission de l'uranium.
P_nlf la probabilité que les neutrons rapides ne fuient pas (non leak fast)
P_nlth la probabilité que les neutrons thermiques ne fuient pas (non leak thermic)
p la probabilité des neutrons qui échappent à l'absorption par le modérateur
f la probabilité que les neutrons thermiques ne soient absorbés ni par la structure du réacteur, ni par le caloporteur ou par le modérateur (c'est la fraction de neutrons utiles)
η la probabilité d'avoir une fission après absorption

Nous obtenons donc l'équation suivante:

n/n₀= ε.f.η.p.P_nlf.P_nlth= Keffectif (Keff)

avec n le nombre de neutrons émis par le combustible (U²³⁵ et U²³⁸) etn₀le nombre de neutrons envoyés initialement. Keff est donc le rendement de la fission au niveau des neutrons. Pour que le nombre de neutrons envoyés soit celui récupéré, il faut que Keff soit égal à 1.

Keff = 1 => réacteur critique
Keff < 1 => réacteur sous critique
Keff > 1 => réacteur sur critique

Pour garder le contrôle de la réaction, on doit rester dans le cadre d'un réacteur critique. Les électrons en excès seront absorbés par les modérateurs, plongés plus ou moins au coeur du réacteur, en fonction de la quantité de neutrons que l'on veuille absorber. Les modérateurs, encore appelés barre de contrôle, sont constituées de Cadmium, de bore ou de cobalt (on obtient du cobalt 60 qui est ensuite revendu aux hôpitaux (traitement du cancer) ou aux industries de conditionnement des aliments (on expose les aliments, ce qui tue tout ce qui est vivant à l'intérieur)).

La mesure du Keff est effectuée avec des barres de platine. On compte les neutrons par unité de surface et de temps, ce qui permettra de contrôler le nombre de neutrons dans le réacteur, et de s'approcher ainsi d'un Keff unitaire.

On utilise aussi une autre variante du Keff: Si on suppose un réacteur idéal de taille infinie: On à alors P_nlf et P_nlth égaux à 1 (pas de fuites de neutrons vers l'extérieur du système).Cela nous donne la formule à 4 facteurs de Keffectif:

K_∞ = ε.f.η.p

Pour avoir un Keff de 1, il faut que le réacteur contienne une masse critique de combustible.

Types de réacteurs, principes technologiques

Pour résumer, le procédé nucléaire consiste en une réaction en chaîne : génération des neutrons - ralentissement des neutrons - diffusion - absorption.

Pour avoir une réaction en chaîne, il nous faut :
- un Keff de 1
- une masse critique de combustible.

Il y a deux types de réacteurs:
- Homogène : le combustible est dissout dans un liquide comme l'acide sulfurique.
- Hétérogène : On a le combustible, le modérateur (liquide (eau légère, lourde, fluides organiques) ou solide (graphite comme Tchernobyl) et le caloporteur.

Schéma du système:

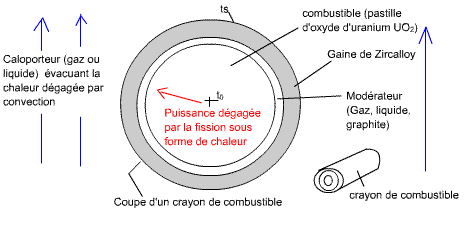
Fig. ? : crayon de combustible, encore appelé pastille de combustible, de la longueur du réacteur

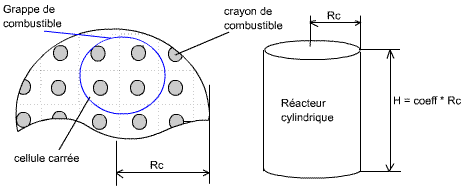
Fig. ? : réacteur nucléaire, rempli de crayons de combustible, qui peuvent être rassemblés en grappes

C'est entre les crayon que circule le caloporteur, chargé d'amené la chaleur jusqu'à la partie thermique de la centrale, pour chauffer la chaudière et produire la vapeur surchauffée.

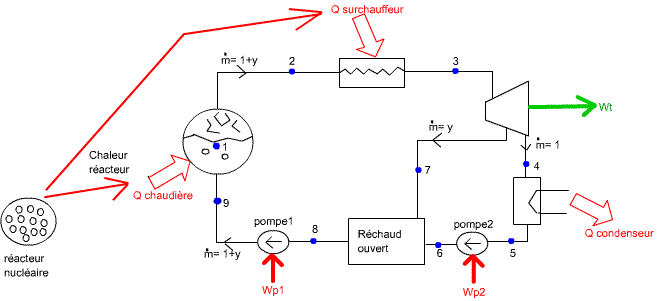
Fig. ? : réacteur nucléaire, son emplacement dans la centrale nucléaire

 

Taille critique du réacteur

Puissance dégagée par la fission

On définit le taux de réaction par : nb de fissions / cm³.s = Σf (1/cm) Θ (neutrons / cm².s)
avec Σf la section efficace macroscopique et Θ le flux de neutrons que l'on envoie contre la surface du système. Θ = n . v , n étant la densité neutronique (nb neutrons / cm³) et v la vitesse du neutron (cm/s).

Le nombre de fissions par unité de temps (par secondes) est donné par : volume (cm³) . section efficace macro (1/cm) . flux neutronique (nb neutrons/cm².s) = V. Σf . Θ = nb fissions / s.

Or une fission produit ΔE (J), en général 200MeV soit 3,2.10^-11, ce qui nous donne la puissance totale P (Joule / s) produite par un volume V de combustible :

P = V. Σf . Θ . ΔE

 

On peut encore écrire l'équation précédente sous la forme:
P = V.N.σf.Θ.ΔE car S = N.σf, avec N le nombre d'atomes par cm³. On a V.N = mf (masse d'atomes fissiles) * 0,6023.10₂₄ (nombre d'avogadro) / 235 (masse atomique de l'uranium 235, en g/mole)

Voir l'exemple p 21.

Quantité de chaleur émise Q = densité de puissance de la fission = p (W/m³), si l'on considère que α, la fraction de puissance de la fission récupérée sous forme thermique, soit de 1 (alors qu'il est de 0.95 normalement). Q= α * p

Chaleur dégagée par la fission

Si l'on multiplie la densité de puissance p (en W/m³) par le volume du combustible (sous forme de barreau cylindrique en général, en m³, V = (π * D² / 4) * 1m de long), on obtient la quantité de chaleur Q émise par seconde (en W). La longueur du barreau est en général de 1m. Si l'on divise la quantité de chaleur produite qui doit être évacuée via la paroi latérale du combustible (de surface S_l = π * D * 1m de long) par cette surface latérale, on obtient alors le flux de chaleur φ (W/m²).

Bilan neutronique

Il faut maintenir la population des neutrons avant et après la réaction. Ce bilan va permettre de déterminer la dimension critique du réacteur.

 

 

Détermination de l'absorption

 

 

 

Transfert de puissance

Limites thermiques de l'échange de chaleur

 

Calculs de transferts thermiques

Il faut tout d'abord connaître les différents flux de chaleur qui sortent des cylindres, sachant que Q est toujours le même, seule la surface latérale augmente plus on s'éloigne du centre et dionc que le rayon augmente.

Equation de conduction pour un barreau cylindrique plein, de rayon R, avec r un rayon quelconque partant du centre (r=0 au centre du cylindre), coefficient de conductivité thermique λ (W/mK), t_surf la température sur la paroi extérieure du cylindre, et p la densité de puissance en W/m³.
t(r) = t_surf + (1/4.λ) p ( (R)² - r² )

Equation de conduction pour un cylindre creux, avec ϕ1 le flux de chaleur provenant de l'intérieur du cylindre (donc Q divisé par la surface latérale intérieure du cylindre) et traversant la paroi (donc φ2 le flux de chaleur sortant du cylindre, c'est à dire de sa surface latérale extérieure):t(r) = t_surf + ( φ1 * R1 / λ ) ln ( R2 / r )
Avec R1 le rayon intérieur et R2 le rayon extérieur, les autres comme pour le cylindre plein.

Equation de convection de Newton: φ (W/m²) = h (t_paroi - t_∞)

 

 

 

Système à deux cycles

 

 

 

Le réacteur CANDU

 

 

Les échangeurs de chaleur

Rappels de thermique et présentation du problème

 

VI.2) Conduction dans un cylindre plein

 

VI.3) Conduction dans un cylindre creux

 

VI.4) Convection forcée

Calcul des températures

 

Mélange diphasique

 

Assèchement

 

Caléfaction

 

 

Exercices

N.B. : Les chiffres en gras sont ceux qui ne sont pas fournis dans l'énoncé, ou extrapolés dans une unité plus pratique que celle fournie.

Problème n°1:

Le combustible d'un réacteur nucléaire est formé de crayons d'uranium métallique ayant 1,27 cm de rayon, arrangés dans une géométrie carrée, avec une distance l entre chaque crayon de 15 cm (voir figure 1).

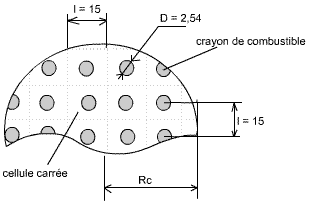
Fig. 1: Distribution partielle des crayons dans un réacteur cylindrique (dimensions en cm)

Le réacteur cylindrique possède un rapport de profondeur (H) / diamètre (2 Rc) de 1,2. Ce qui nous donne une hauteur H du cylindre de H = 2,4 Rc.

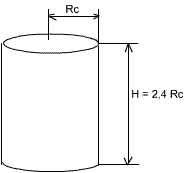
Fig. 2 : Réacteur cylindrique

D'après les propriétés nucléaires, le Laplacien "Buckling" à été estimé à Bc² = 8,6 (1/m²).

On donne les valeurs suivantes:
- Densité de l'uranium métallique : ρ_u = 19.10³ kg/m³
- La placien "Buckling" pour un réacteur cylindrique: Bc² = ( 2.405 / Rc )² + ( π / H )²

a) Calculer le rayon critique du réacteur

Soit Bc² = ( 2.405 / Rc )² + ( π / 2,4Rc )² = 8,6 => 8,6 = [ 2,405² + (π² / 2,4²) ] / Rc²

=> Rc² = [ 2,405² + (π² / 2,4²) ] / 8,6=> Rc = 0,9337 m = 93,37 cm

b) Calculer le nombre estimé de crayons que doit contenir le coeur du réacteur

Un crayon prend la surface de l'enveloppe de section carrée qui l'entoure. La surface occupée par un crayon est donc de 15*15 = 225 cm².

La surface offerte par la section du réacteur cylindrique de Rc = 93 cm est :
π Rc² = 27 388,27 cm².

En faisant une grosse approximation, on peut dire que le nombre de crayons pouvant être logés dans le réacteur est de :
Surface réacteur / Surface crayon = 121,72.

En première approximation, on peut estimer à 121 le nombre de crayons que l'on mettra dans le réacteur.

c) Calculer la masse critiquedu combustible nécessaire pour que la réaction en chaîne puisse être maintenue.

En prenant le nombre de crayons trouvés précédemment, et en multipliant par le volume d'un crayon de combustible, nous trouvons le volume critique, duquel on déduit la masse critique en multipliant par la masse volumique de l'uranium métallique, qui est le constituant d'un crayon.

Surface de la section d'un crayon: π * 1,27² = 5,067 cm². La longueur du crayon est celle du réacteur, c'est à dire 2,4 * Rc = 224,08 cm. Ce qui nous donne le volume d'un crayon, qui est de 1135,47 cm³, soit 1,13547.10^-3 m³.

Pour 121 crayons, cela nous fait un volume critique de 1,13547.10^-3 * 121 = 0,137391949 m³

En multipliant par la masse volumique ρ_u : 0,137391949 * 19.10³ = 2610,447 kg.

La masse critique mc du réacteur est donc de : mc = 2,6 tonnes.

 

---

Problème n°2:

Un crayon de combustible d'un réacteur nucléaire à eau pressurisée à les dimensions indiquées dans la figure 2.

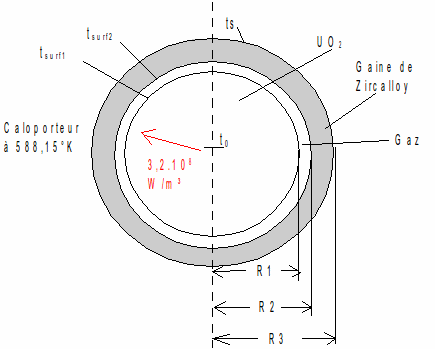
Fig. 3: Crayon de combustible

Avec les rayons suivants: R1 = 4,09.10^-3 m, R2 = 4,18.10^-3 m et R3 = 4,75.10^-3 m.

La température moyenne du caloporteur baignant le crayon est de 315°C, soit 588,15°K.
La densité de puissance produite par la fission est p = 3,2.10⁸ W/m³.
On possède les informations suivantes sur le système:
- Conductivité thermique de :

* Zircalloy : k_z = 13 (W/m.K)
* Oxyde d'Uranium : k_UO2 = 2,8 (W/m.K)

- le coefficient de transfert de chaleur dans le caloporteur: h = 34.10³ (W/m².K)
- La conductance thermique de la couche gazeuse: h_g = 6000 (W/m².K)

Déterminer la température t₀ au centre du combustible et la température ts à la surface extérieure de la gaine.

On connait la densité de puissance émise par le coeur, on peut donc déterminer par les équations de la conduction la différence de température entre la surface et le coeur du matériau. Si l'on connait la température à la surface on connait donc la température au centre.
On connait la température du caloporteur, on peut donc retrouver la température à la surface par l'équation de la convection forcée.

Quantité de chaleur émise = densité de puissance de la fission = p (W/m³), si l'on considère que α, la fraction de puissance de la fission récupérée sous forme thermique, soit de 1 (alors qu'il est de 0.95 normalement).

• Différence de température entre t₀ et ts :

Il y a tout d'abord conduction de la chaleur à travers la pastille d'uranium, ensuite convection à travers la couche gazeuse, puis de nouveau conduction à travers la paroi de la gaine en Zircalloy.

Calculs intermédiaires des flux de chaleur:

- La quantité de chaleur Q contenue dans le barreau d'UO₂ vaut : Q = p (W/m³) * volume du barreau d'UO₂ de longueur unitaire (m³) = 3,2.10⁸ * (π * R1² * 1) = 16 816,92 W

- Le flux de chaleur ϕ1 (W/m²) qui sort du barreau d'UO₂ est :
ϕ1 = Q / surface latérale du barreau de longueur unitaire.
ϕ1 = 3,2.10⁸ * (πR1² * 1) / (π2 * R1 * 1) = (3,2.10⁸ * 4,75.10^-3) /2 = 760 kW/m²

- Le flux de chaleur ϕ2 (W/m²) qui sort de la couche gazeuse est :
ϕ2 = Q / surface latérale de la couche gazeuse de longueur unitaire.
ϕ2 = Q / (π * 2 * R2 * 1) = 16 816,92 / (π * 2 * 4,18.10^-3) = 640,31 kW/m²

- Le flux de chaleur ϕ3 (W/m²) qui sort de la gaine de zircalloy pour se retrouver dans le caloporteur est :
ϕ3 = Q / surface latérale de la gaine de longueur unitaire.
ϕ3 = Q / (π * 2 * R3 * 1) = 16 816,92 / (π * 2 * 4,75.10^-3) = 563,4728 kW/m²

- Conduction dans la pastille d'Uranium. On se sert de l'équation de la conduction à travers un cylindre plein (voir questionf) du problème 3) au rayon r=0 pour se placer au centre :
ΔT1 = ( t₀ - t_surf1 ) = (1 / 4k_UO2 ) p ( R1² ) = ( 3,2.10⁸ * (4,09.10^-3)² ) / (4*2,8) = 477, 946 ° (K ou C, puisque c'est une différence de température).

- Convection dans la couche gazeuse. On se sert de l'équation de Newton:ϕ = h (t_paroi - t_∞)
ΔT2 = ( t_surf1 - t_surf2 ) = ϕ1 / h_g = 760 000 / 6000 = 126,66 ° K

- Conduction dans la gaine de zircalloy. On se sert de l'équation de la conduction à travers la paroi d'un cylindre creux:
ΔT3 = ( t_surf2 - ts) = ( ϕ2 * R2 / k_z ) ln ( R3 / R2) = [ 640,31.10³ * 4,18.10^-3 / 13] ln (4,75 / 4,18) = 26,31889 ° K

On peut donc en déduire la différence de température entre le centre du barreau et la surface de la gaine: ( t₀ - ts ) = 477, 946 ° + 126,66 ° + 26,31889 ° = 630,925 ° K

• Température à la surface ts:

Convection dans le caloporteur : ts = t_caloporteur + (ϕ3 / h) = 588,15°K + (563,4728 / 34) (on divise de kilo par des kilo) = 604,72 ° K = 331.57 °C

• Température au centre t₀ :

t₀ = ts + 630,925 = 962,498 °C

 

---

Problème n°3:

Une pastille d'oxyde d'uranium (UO₂) enrichi contient 2,9% d'uranium 235 (₉₂U²³⁵) et le reste en uranium 238 (₉₂U²³⁸) soit 97,1%.
La pastille à un diamètre de 8,19.10^-3 m, et sa densité ρ = 10,2.10³ kg/m³.

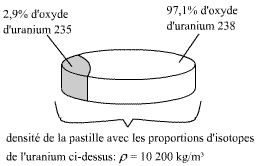
Fig. 4 : Pastille d'oxyde d'uranium enrichie

Masse molaire du mélange dans les proportions précitées d'U235 et d'U238 pour la molécule de UO₂: 0,27 kg/mole
La molécule de U²³⁵O₂ est plus légère que celle de U²³⁸O₂ car elle à 3 neutrons en moins. Il y a donc plus de molécules de U²³⁵O₂ dans un kilogramme que il n'y a de molécules de U²³⁸O₂. La densité et la masse moléculaire fournies tiennent compte de ce fait.

On donne les valeurs suivantes:
- Section efficace de fission de l'U²³⁵ : σ_f = 360 barns (1barn = 10^-28 m²/atome) = 3,6.10^-26 m²/atome
- Nombre d'Avogadro : Na = 6,02.10²³ molécules par mole.
- Energie libérée par chaque fission : ΔE = 200MeV = 200.10⁶ (eV) * 1,6.10^-19 (J/eV) = 3,2.10^-11 J

a) Calculer le nombre de molécules d'UO₂ / m³, N_UO2.

On sait que pour les proportions de 2,9% de U²³⁵O₂ et de 97,1% de U²³⁸O₂, la densité est de ρ.

Nombre de molécules / kg: Na (molécules/mole) / A (kg/mole).

On multiplie ensuite par la densité ρ: (Na/A) (molécules/kg) * ρ (kg/m³) pour obtenir le nombre de molécules de l'espèce UO₂ (avec les deux isotopes d'uranium) par unité de volume, N_UO2.

N_UO2 = (Na / A (UO₂) ) * ρ = 6,02.10²³ * 0,270 * 10,2.10³

N_UO2 = 2,2742222.10²⁸ molécules/m³

b) Calculer le nombre d'atomes d'U235 / m³.

D'après la formule chimique de l'oxyde d'uranium, pour une molécule d'UO₂ correspond un atome d'uranium. Il nous faut donc connaitre le nombre N_U235 de molécule de U235O₂, sachant que l'on a 2,9% de cette molécule dans 1 m³ de molécules d'UO₂ .

N_U235 = (nb molécules de UO₂ /m³) * 2,9% = (Na / A (UO₂) ) * ρ * 0,029

N_U235 = 6,02.10²³ * (0,029 / 0,27) * 10,2.10³ = 6,595244444.10²⁶ atomes/m³

c) Calculer la section efficace macroscopique Σ.

On néglige l'effet des autres atomes dans la fission, seuls les atomes d' U235 interviennent.

Σ = σ.N = m²/atomes * atomes/m3 = 3,6.10^-26 * 6,595244444.10²⁶ = 23,74288 m^-1

1/Σ = 0,042117889 m = 4,21 cm

d) Calculerla densité de puissance p.

La pastille est soumise à un flux de neutrons thermiques (susceptibles donc d'être absorbé) d'intensité I = 4,1.10¹⁷ neutrons/(m².s).

p (J/m³s) = Σ (1/m) . Φ (n/m²s) . ΔE (J) = 23,74288 * 4,1.10¹⁷ * 3,2.10^-11

p = 3,1150659.10⁸ W/m³

p = 311,5 MW/m³

e) Calculer le flux de chaleur ϕ.

Quantité de chaleur émise = densité de puissance de la fission = p (W/m³), si l'on considère que α, la fraction de puissance de la fission récupérée sous forme thermique, soit de 1 (alors qu'il est de 0.95 normalement).

Par unité de longueur (1m), la pastille aura un volume V = (π * D² / 4) * 1 (avec D le diamètre de la pastille d'uranium). Sa surface latérale sera S_l = π * D * 1.

Une pastille de 1m de long émettra donc une quantité de chaleur en W de p (W/m³) * V (m³), et cette quantité de chaleur sera émise à travers une surface S_l , soit pV (W) / S_l (m²), ce qui nous donne le flux de chaleur ϕ.
Flux de chaleur ϕ (W/m²) = (p*V) / S_l = (p * π * D² / 4 ) / (π * D) = P * D / 4

ϕ = 311,5.10⁶ * 8,19.10^-3 / 4 = 637 796.25 W/m² = 637,8 kW/m²

f) Calculerla différence de température entre la surface externe t_surf et le centre de la pastille t_centre.

Le coefficient de conductivité thermique λ de l'oxyde d'uranium est de 2,8 W/mK.

On a l'équation de conduction suivante:
t(r) = t_surf + (1/4λ) p ( (D/2)² - r² ). Si l'on se place au rayon r = 0 (au centre), on obtient l'équation suivante:

ΔT = ( t_centre - t_surf ) = (1 / 4λ) p ( D² / 4 ) = (p*D / 4) * D/4λ =ϕ * D/4λ
ΔT (K) = ϕ (W/m²) * D (m) / 4λ(W/mK)

Donc ΔT = (637 796.25 * 8,19.10^-3) / (4 * 2,8) = 466,388 K = 466,388 °C

Car c'est une différence de température, et l'échelle des Kelvins et des °C est la même.

à suivre...