Couple & puissance

Sommaire de la page

---

Préambule

Une des choses les plus importante à comprendre est la notion d'énergie que l'on peut tirer du moteur, et sous quelles formes. Nous allons donc voir les notions de couple et de puissance utilisées un peu à tort et à travers, sans qu'elles soient parfaitement comprises.

Les notions ci dessous font appel à de la mécanique de base, mais exprimé, je l'espère, assez simplement pour être compris même de ceux qui ont un faible bagage mathématiques. Pour ceux qui ont compris la notion de couple et de puissance sous forme d'équations mathématiques, il peut être bon me semble-t-il de revoir cela exprimé sous forme littéraire de vulgarisation, comme je vais essayer de le faire plus bas.
Comme il y a beaucoup de notions à ingurgiter d'un coup, je vous invite à lancer les neurones si vous voulez tout comprendre, et à y relire plusieurs fois.
Vous pouvez sauter directement au résumé de la page pour voir les notions principales à retenir.

Notion de travail et de puissance

Pour aborder la notion de puissance, je commencerais tout d'abord par la définition générique de la mécanique.

Notion de travail ou énergie

Pour transporter une valise dans un escalier en montant, on doit fournir de l'énergie. Cette énergie permet de combattre la pesanteur terrestre, qui tend, elle, à faire descendre la valise.
Cette énergie fournie est appelée un travail, et est exprimée en Joule (J). C'est une force multipliée par la distance parcourue dans la direction de la force (ici une hauteur à grimper). Le Joule est donc 1 Newton (unité de la force) multiplié par 1 mètre (unité de la distance).
En effet, au départ on ne fournit pas directement de l'énergie, mais une force de traction vertical vers le haut. La pesanteur terrestre elle non plus ne fournit pas d'énergie, mais une force de gravitation verticale vers le bas (F_g=mg). C'est le déplacement de la valise, dans la direction de la force uniquement (si on ne monte pas l'escalier mais qu'on marche sur le plat on n'effectue pas de travail à proprement parler), qui génère un travail.
Dans le cas de la valise à emmener en haut de l'escalier, la formule qui nous donne le travail à effectuer est donnée par la force à appliquer (F_g force de gravitation = m.g) multipliée par la distance selon laquelle s'exerce cette force, c'est à dire uniquement la hauteur de l'escalier, la longueur sur l'horizontale de l'escalier ne comptant pas car la force de gravitation F_g n'est orientée qu'en verticale :

Travail = m.g.h

Donc seules la masse m de la valise (en kg) et la hauteur h à grimper (en mètres) interviennent, la pesanteur g restant constante.
C'est pourquoi, que l'on monte l'escalier en courant, en marchant, que l'escalier ait une pente de 60 % ou de 5 %, le travail sera toujours le même pour monter la valise en haut de l'escalier. On dit que le travail est indépendant du chemin parcouru, mais dépend uniquement du point de départ et du point d'arrivée (on aurait très bien pu monter et descendre plusieurs fois l'escalier, que le travail resterait inchangé, le travail récupéré lors de la descente de l'escalier étant égal à celui fourni pour le monter).

Notion de puissance

Le fait de monter vite ou pas l'escalier implique un effort supplémentaire de notre part, effort non pris en compte dans la notion de travail. Il nous faut donc aborder la notion de puissance.
Si l'on divise le travail par le temps mis à monter l'escalier, l'on obtient une puissance. Cette puissance s'exprime en J/s (Joule par seconde). C'est en gros le travail fourni pendant une seconde. Une puissance est donc un travail instantané.
La formule de la puissance à fournir pour monter un escalier est la suivante :

puissance P = (m.g.h)/t

Ici, la puissance à fournir dépend du temps t mis pour monter l'escalier. Plus on voudra le monter vite (t petit) et plus il faudra fournir de puissance (le terme mgh de la formule, divisé par une valeur plus petite, se trouve moins diminué! Donc P est plus important).

Ce qu'il faut retenir, c'est que le travail est une énergie fournie (en J), la puissance une énergie fournie par unité de temps (en J/s).

La puissance, exprimée en J/s, est plus souvent exprimée en Watts (W).

Aller, on va revoir tout ça sous une autre forme.
L'énergie ou le travail réalisé est une force appliquée sur telle distance. On peut donc voir la force comme une énergie par unité de distance (le mètre), c'est à dire l'énergie à communiquer à un objet pour le déplacer. S'il faut le déplacer sur 10 m, cette énergie pour le déplacer d'1 m sera à exercer 10 fois, ce qui donne l'énergie totale du déplacement (E=F.d). L'énergie unitaire de distance (J/m) ou force (N) pour déplacer un objet sera à exercer tout le long du trajet.
La puissance est comme la force, une énergie unitaire, mais par unité de temps cette fois-ci. Pour réaliser un trajet, on sait qu'on doit appliquer à l'objet telle énergie, sans se préoccuper du temps pour faire le trajet.
Si le trajet se fait dans un temps très long, la quantité d'énergie à appliquer (ou force aussi) par unité de temps (la seconde) sera très faible, car on aura le temps de donner plein de petites impulsions. C'est le petit enfant qui pousse une voiture, qui va la faire bouger de 10 cm puis tout essouflé, va reprendre sa respiration pendant 30 s. La puissance (énergie par seconde) nécessaire est faible.
Si le trajet se fait sur un temps très court, il faudra appliquer toute l'énergie en un temps très court, donc fournir beaucoup de puissance. Là où le petit enfant mettra 10 minutes pour faire 10 m, l'adulte costaud qui pousse fort et sans s'arrêter va mettre 5 s.

Autre expression de la puissance :
La puissance est une énergie par seconde, soit P = E/t, avec E étant une force multiplié par la distance durant laquelle s'exerce cette force, soit E = F . d.
On peut donc écrire la puissance comme étant le produit d'une force par la vitesse de déplacement, c'est à dire l'énergie dépensée sur la distance parcourue pendant une seconde.
P = E / t = F. d/t = F(N).V(m/s)
Cette expression est rigolote quand on mesure la force aérodynamique qui s'oppose au déplacement de la voiture, cette force dépendant de la vitesse au carré (V²), donc la puissance à dissiper pour vaincre cette force est fonction de V².V donc V³!

Pour résumer

La puissance est définie comme une énergie fournie, divisée par le temps durant lequel est cette énergie. Plus le temps mis pour monter l'escalier sera court, plus la puissance devra être élevée (on divise le travail par une valeur plus faible).
Pour monter une valise dans un escalier, le travail sera toujours le même, mais la puissance va varier suivant que l'on monte vite ou doucement. La puissance peut à ce moment là être vue comme un débit d'énergie, plus la puissance est élevée et plus le débit (quantité d'énergie fournie en 1 seconde) est élevé lui aussi.

Application à la méhari

Revenons maintenant à la méhari. Faisons lui monter une côte (oui je sais, elle aime pas ça). Le moteur doit donc fournir de l'énergie afin de contrer l'action de la pesanteur. La pesanteur s'exerçait tout à l'heure sur la valise, mais maintenant la valise c'est la méhari+chauffeur+bagages. Nous avons donc une valise un peu plus lourde.
Que le moteur ai une puissance de 9 cv (puissance des premières 2cv, soit 6.6 kW) ou de 29 cv (puissance des dernières méhari, soit 21.3 kW), le travail à fournir par le moteur sera le même pour les deux moteurs, et ainsi la voiture montera la pente quelle que soit la motorisation qui la tracte. Par contre, le moteur de 21 kW montera la côte beaucoup plus vite que le moteur de 7 kW (car il mettra moins de temps à fournir le même travail).

Forces s'opposant au déplacement

Lorsque la voiture est sur le plat, il y a un travail a réalisé au démarrag et à l'accélération pour vaincre l'inertie de la masse de la voiture.
Une fois la vitesse désirée atteinte, on arrête d'accélérer, il n'y a plus aucun travail à effectuer pour la pousser à vitesse constante une fois qu'elle est lancée (la force d'inertie due à l'accélération du démarrage est donc nulle).
Vous avez essayé, et vous devez faire un effort quand même?
Bienvenue dans le monde réel, celui des pertes par frottement. L'énergie à fournir pour vaincre ces frottements est autant d'énergie gaspillée par le moteur inutilement. Sans les frottements, une méhari lancée à 80 km/h sur une route plate roulerait indéfiniment, moteur coupé, car il n'y a pas de travail à fournir (pas de forces s'opposant horizontalement).
Mais malheureusement il y a des frottements générés par le déplacement (frottement des molécules de l'air sur la carrosserie, enfoncement du pneu à chaque rotation qui nécessite un effort, roulements avec les billes qui frottent en roulant, etc.). Et comme il y a quand même une force à appliquer à chaque instant, il y a un travail à fournir.

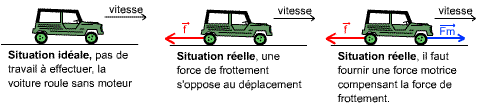
Fig 1: illustration de la notion de frottements

Comme il y a des frottements (force parallèle au déplacement de la voiture, dans le sens opposé), il nous faut mettre en route le moteur, donc fournir de l'énergie pour faire avancer la voiture. Comme on fournit une force dans la direction du déplacement, on fournit un travail. Ici le travail est la force de frottement à combattre (grâce à la force Fm) multipliée par la distance horizontale parcourue par la voiture.

Pour illustrer la notion de travail, nous pouvons prendre l'exemple suivant : la méhari monte toujours une côte, mais cette fois ce n'est plus le moteur qui tire, mais nous qui poussons (la côte est une faible pente. La méhari est légère, mais faut pas pousser !!!).
Lorsque la voiture grimpe une côte, il faut fournir un travail pour vaincre la gravitation. L'énergie de pesanteur pour monter un objet de masse m sur une hauteur de h mètres est donnée par la formule E=m.g.h, comme vu précédemment. Si vous intercalez une balance entre vos mains et la voiture, vous voyez une masse m s'afficher au cadran. Cette masse m multipliée par la gravitation g nous donne la force motrice que l'on doit produire pour combattre à la fois la force de gravitation ainsi que la force de frottement. En multipliant par la distance parcourue, on obtient ainsi le travail moteur que nos petits bras doivent fournir pour faire monter la voiture. Ce travail est supérieur à celui pour combattre la force de gravitation, à cause des frottements que l'on prend en compte.
Evidemment, plus la pente est importante, et plus la masse m indiquée par la balance sera élevée, mais plus la distance à parcourir sera courte. Par contre, à cause des frottements, le travail n'est plus indépendant du chemin parcouru.
Au fait, pourquoi cette force de gravitation intervient en côte et pas sur le plat? Sur le plat, cette force est dirigée vers le bas, donc perpendiculaire à la voiture, pas de travail car pas de force dans le plan de déplacement. En côte, le plan de déplacement n'est plus horizontal, il apparait donc une composante de le force dans ce plan. Cette composante est une force dirigée dans le sens opposé au déplacement pour une montée (donc travail négatif s'opposant à l'avancement) et dans le même sens pour une descente, donc en descente cette force nous entraine vers le bas, il faut donc augmenter la force de frottement pour conserver une vitesse raisonnable (action sur les freins).

Nous venons de voir les énergies nécessaires pour faire se déplacer la voiture, qui sont des énergies de translation. Nous devons fournir un travail ou énergie pour faire se déplacer la voiture, et il faut fournir d'autant plus de puissance que l'on veut que ce travail soit effectué dans un court laps de temps.
Or, cette énergie de translation est d'abord obtenue par une énergie de rotation, l'énergie appliquée sur les roues. L'énergie de rotation est ensuite transformée en énergie de translation via l'interface sol/roue. Nous verrons dans le paragraphe suivant comment l'on peut exprimer ces énergies de rotation.

Travail et puissance de rotation

Abordons maintenant la puissance sous un autre angle, c'est à dire l'énergie délivrée par la rotation du moteur.
Archimède à dit: "Donnez moi un levier suffisamment long et un point d'appui, et je soulèverais le monde". Cette phrase illustre le principe du levier, à savoir que une force exercée sur une barre possédant un point de rotation exerce sur le centre de rotation un moment, c'est à dire un couple tendant à faire tourner la barre autour de ce point. En contrepartie, un moment exercé en ce point induira une force sur le levier.
Un moment s'exprime en N.m (Newton.mètre), c'est à dire que c'est une force (en Newton) multipliée par la distance (en mètres) prise perpendiculairement entre la direction de la force et le point de rotation.

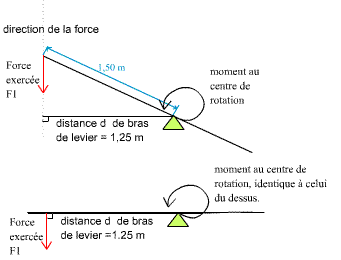
Fig 2: L'application d'une force sur un point engendre un moment sur tous les autres points

Fig 3: l'intensité du moment engendré par une force dépend de l'intensité de la force et de la distance.

De la distance d'application de la force dépend donc l'intensité du moment appliqué. Cette distance est appelée bras de levier.
Le moment est aussi une énergie, c'est à dire un travail, qui peut s'exprimer en Joule. Mais attention, un moment est l'énergie à fournir pour faire tourner de 1 radian (un radian étant à peu près égal à 60°). Nous voyons donc que la notion de couple moteur (le moment exercé par le moteur) est en fait le travail que peut fournir celui-ci pour tourner de 60°, sans tenir compte du temps.
Nous pouvons faire le lien entre la force linéaire en N et le couple en N.m, qui sont tous les 2 une énergie appliquée sur une unité de distance. F étant en J/m, et C étant en N.m / rad, le radian n'étant pas une unité ne s'écrivant pas. Attention à ne pas confondre le N.m de rotation (N.m/rad en fait) avec le Joule qui est aussi des N.m (force linéaire par distance).

Pour obtenir l'énergie ou travail à appliquer sur le levier pour le faire tourner de x radians, il faut mulitiplier par le nombre de radians.
E(J) = Couple (N.m/rad) * déplacement angulaire ou angle de rotation (rad).
On pourrait exprimer l'energie en N.m plutôt que J, de même que le radian étant adimensionnel on pourrait exprimer un couple N.m/rad en J. Mais on ne le fait pas pour ne pas risquer de perdre des lecteurs!

En somme, le couple est l'énergie à appliquer pour faire tourner le levier de 1 radian, comme la force est l'énergie pour faire avancer de 1 m.
Quand on dit N.m, les mètres ne sont pas le déplacement d'un objet mais le bras d'un levier.
Et pour éviter de confondre, on évite de dire qu'un travail linéaire F.d est en N.m, mais en J, pour réserver N.m au couple (qui en fait est en N.m/rad).

De par la définition du moment (force multipliée par la distance), plus la force exercée est distante du point de rotation, et plus le moment exercé sera important. De même, plus la force est importante, plus le moment est important.
Prenons l'exemple suivant : je place la méhari au bout de l'extrémité la plus longue du levier. Son poids de 600 kg, sous l'effet de la pesanteur terrestre, va exercer une force vers le bas au bout du levier. Cette force va induire un moment au niveau du point de rotation qui va faire pencher le levier vers la droite.
Maintenant, je place à l'autre extrémité un camion, d'un poids de 6000 kg. Son poids va exercer une force, qui va induire un moment au centre tendant à faire basculer le levier vers la gauche. Seulement voila, le moment engendré par le camion est contrarié par celui de la méhari. Qui va gagner ???
Sur le dessin ci dessous, l'on voit que la balance penche en faveur de la méhari.

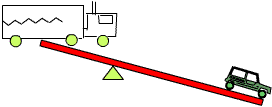
Fig 4: Une méhari plus lourde qu'un camion?!!!

Pour ce faire, vu que la force exercée par la méhari est 10 fois plus faible que celle du camion, il nous faut donc une distance 10 fois plus grande entre la voiture et le point de rotation que celle du camion au pivot. Ainsi, même si la méhari est plus légère, elle exercera un moment supérieur au camion. Si l'on remplace le camion par la terre, et que l'on allonge considérablement le levier, la méhari soulèverais le monde...

On peut aussi voir la chose d'une façon différente. La méhari va exercer une force plus faible, mais sur un distance plus grande. on peut parler en longueur de bras de levier, mais aussi en distance pour faire bouger de 1°, la distance à parcourir valant angle en radian multiplié par le rayon (ainsi, pour un angle de 360 ° soit 2π radians, on connait la circonférence du cercle qui est de 2πR comme tout bon écolier le sait), plus on est loin du centre et plus la méhari se déplace pour faire bouger d'un degré. En étant 10 fois plus loin que le camion, elle se déplacera 10 fois plus. Le couple étant force multipliée par la distance, la méhari exerce un couple plus important que celui du camion, même si la force est moins grande. Si on parle en terme d'énergie c'est la même chose, l'énergie de la méhari l'emporte sur le camion.

C'est le même principe qui s'applique lorsque l'on dévisse un boulon vissé à fond: si l'on prend le boulon avec les doigts et que l'on essaye de le dévisser, on applique directement un moment au point de rotation. Mais nous ne sommes pas assez fort pour générer un moment (ou énergie) suffisant pour dévisser. Si l'on place une clé, on n'exerce non plus un moment sur le centre de rotation mais une force. Si l'on se place à l'extrémité de la clé, la force nécessaire pour produire le moment de dévissage au point de rotation est suffisamment faible pour être fournie par nos petits muscles.
A noter que quand on prend le boulon avec les doigts, l'on n'exerce pas un moment mais bien un couple de force, tendant à faire tourner le boulon. Malheureusement le bras de levier dont nous disposons alors est celui de la tête de boulon, ce qui n'est pas suffisant pour exercer le moment nécessaire au desserrage du boulon.
Quand le boulon est presque entièrement dévissé, le moment nécessaire pour le faire tourner devient très faible, et l'on peut alors le dévisser à la main.

Bon, tout ça c'est juste pour vous entrainer à voir les choses de différentes façons.

A partir de maintenant, je désignerais le moment par le mot couple. Au niveau mécanique, ce terme représente à la fois les deux forces égales, parallèles et de direction opposées exerçant un moment sur un point situé entre les deux forces, mais aussi le moment engendré par ce couple de forces.
Au niveau automobile, on désigne le moment obtenu au centre du vilebrequin par le mot couple moteur.

Au niveau de la puissance, c'est la même chose. C'est l'énergie appliquée au moteur pendant une seconde.
L'énergie appliquée au moteur pour un tour est le couple multiplié par un angle de rotation correspondant à 1 tour (1 tour = 360° soit 2π radians).
La puissance est l'énergie divisée par le temps, donc P = C . (angle / temps). Angle/temps est la vitesse de rotation (encore appelée vitesse angulaire ω).
P (W) = C (N.m/rad) . ω (rad/s)

Attention, la vitesse angulaire est en radians/s, si on veut utiliser les tours/min il faut utiliser la formule suivante :
P(W) = C (N.m) . N(tr/min) . (2π/60)

Vous avez du remarquer dans les fiches techniques de votre véhicule l'indication de puissance du moteur. Celle-ci correspond à la puissance maxi que peut développer un moteur, donc l'énergie maximale qu'il est capable de débiter en 1 petite seconde. Par exemple, le moteur de la deuche est capable de développer la même énergie qu'un V6 de 8 litres, mais dans un temps 10 fois plus long!
Les puissances moteurs s'expriment en kilo Watts (kW) soit 1000 W, et non en cheval vapeur (1kW = 1.36 cv(norme GB)).
A noter que les puissance indiquées pour le moteur sont notées en cv DIN (norme allemande) et en cv SAE (norme américaine). Les chevaux DIN correspondent à la puissance développée par le moteur seul (sans les pertes de transmission et de boite de vitesse) muni de tous ses accessoires (ventilateur, alternateur, etc.) alors que pour les cv SAE, c'est toujours la puissance du moteur seul mais sans les accessoires (donc moins de pertes, c'est pourquoi la puissance SAE est supérieure à la puissance DIN).
C'est la puissance DIN qui est la plus proche de la réalité.

Pour résumer

- le couple moteur (N.m) est l'énergie disponible au centre de rotation du vilebrequin afin de faire le tourner de 1 radian.
- l'énergie ou travail fourni par le moteur est le couple disponible multiplié par le nombre de tours (1 tour = 2π radians) à réaliser pour effectuer ce travail.
- la puissance est le travail instantané, c'est à dire fourni par le moteur en 1 seconde.

L'intérêt de la notion de puissance est de ne pas avoir besoin de connaitre le rapport de transmission final entre le moteur et la roue, cette réduction permettant de réduire le couple du moteur, à condition d'augmenter la vitesse de rottaion moteur. Avec la puissance moteur, on sait directement que ce sera la même puissance appliquée sur les roues (au rendement de boite près).

Dans le cas du moteur, nous avons un vilebrequin qui tourne. Au centre du vilebrequin, c'est à dire au point de rotation, il s'exerce un moment, ou couple, en N.m. C'est de ce couple que provient toute l'énergie nécessaire pour faire avancer la voiture.

Oui mais d'ou vient ce couple me direz-vous. Facile, c'est toujours le même principe du levier. Mais voyez plutôt le schéma suivant:

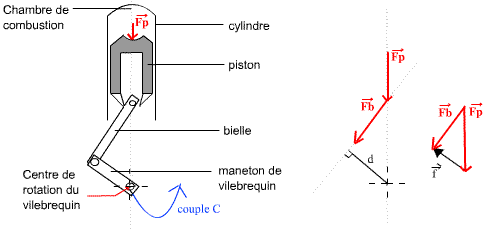
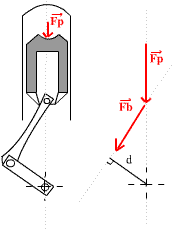
Fig 5: Transformation de la force de pression Fp en moment-couple C sur le vilebrequin

est la force exercée sur la tête de piston par la pression générée lors de l'explosion du mélange. est la force exercée par la bielle sur le maneton du vilebrequin. A cause du frottement piston/cylindre, traduit par la force , est plus faible que . Plus le frottement est important, et plus sera orienté vers le haut, et plus la force sera diminuée par rapprt à . C est le couple résultant de la force multiplié par la distance d.

Dans ce schéma, le vilebrequin est vu depuis la place du conducteur. Il tourne donc dans le sens trigonométrique, c'est à dire dans le sens inverse des aiguilles d'une montre.

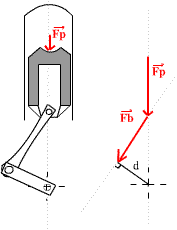
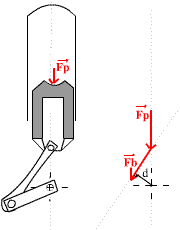
Sur les schémas ci-dessous (Fig 6) des différents instants du temps moteur, on voit que la bielle à pratiquement toujours la même position de porte à faux ce qui fait que elle est soumise à une forte flexion. Ce moment de flexion tend à plaquer le piston contre un bord de la paroi (voir sur la figure qu'il est plus plaqué d'un côté que de l'autre) ce qui entraîne de forts frottements entre la paroi et le piston, qui font diminuer la forces transmises par la bielle, par rapport à la force initiale (voir à droite de la Fig 5). On peut aussi dire que le rendement est de 95% à cet endroit.

Le bras de levier d est lui aussi très faible. Il n'est maximal que quand le maneton fait un angle de 45° par rapport au PMH, et il est même nul au PMH, ce qui fait que lorsque l'explosion se produit, et que la pression est la plus forte, paradoxalement aucun moment n'est appliqué sur le vilebrequin! Et le moment maximal n'est appliqué que lorsque la pression commence à chuter. A noter que à la fin du cycle, la pression est très faible et le bras de levier aussi, ce qui fait que le couple en fin de temps moteur est faible. Le couple le plus important n'est donc fourni que sur pratiquement un tiers de la course de détente.

Fig 6 : Variation du couple fourni en fonction de la position du vilebrequin

On le voit, le système bielle-vilebrequin n'est pas le meilleur pour transformer une translation en rotation, et pourtant on l'utilise depuis plus de 150 ans, et on n'a rien trouver de mieux depuis (tous les autres systèmes posent encore des problèmes de mise en place, voir les birotor Citroën des années 70).

Application pratique du couple et de la puissance

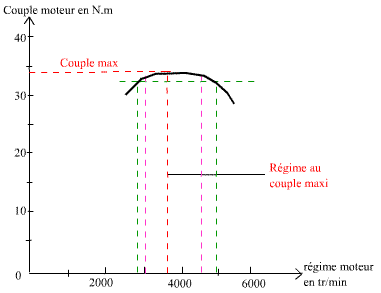
Nous avons donc vu que la puissance était le couple multiplié par le régime de rotation. On voit bien ce couplage entre le couple et la puissance en fonction du régime de rotation sur les courbes de couple et de puissance (fig 7 et 8) :

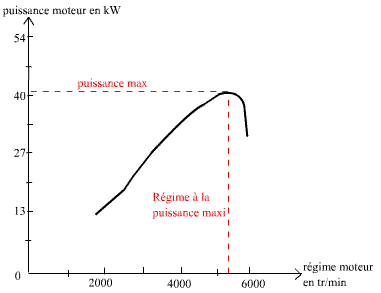
Fig 7: courbe de couple

Fig 8: courbe de puissance

Les deux courbes ci dessus sont inspirées des résultats obtenus par Christian Bosch avec une deuche montée avec un filtre à air de 2cv Cross. Les données ne sont donc pas celles du moteur d'origine, seul l'allure de la courbe ainsi que les régimes doivent être sensiblement proches de l'originale.

La boite de vitesse correspond grosso merdo à un levier, ayant pour but d'amplifier la force exercée par le moteur sur les roues. D'ailleurs le rapport de transmisison est appelé longueur de transmission. Le couple moteur se retrouve lui au centre de chaques roues motrices, divisé par le nombre de roues motrices et diminué des frottements dans les pignons de boite et de transmission. C'est le principe de conservation de l'énergie.

La puissance moteur sert donc à faire accélérer la voiture, dans le temps le plus court possible. Plus il y a de la puissance à la roue, et plus le temps est court. Plus il y a des consommateurs de puissance (nombre de personnes, ampli d'autoradio à fond, côte) et plus ce temps sera long (la puissance du moteur sera perdue en cours de route entre le volant moteur et la roue). J'ai trouvé cette formule sur le site du 2cv club de France, pour calculer la puissance Pu de la voiture fournie à la roue :
Pu (kW) = (P / T³) *319.53
formule issue de l'énergie nécessaire pour vaincre l'inertie d'une masse P (poids de la voiture, outils et conducteur compris) sur un temps T (temps mis pour parcourir 400 m départ arrêté). P en kg et T en s.

Forces s'opposant au déplacement

Les calculs numériques ne seront pas détaillés pour ne pas obscurcir le texte, ils seront retrouvés dans le tableur Open Office Calc trouvé ici, sur la feuille "résistance avancement".

La valeur numérique des forces ne nous intéresse pas ici, car nous regarderons plutôt la notion de puissance (chapitre suivant).

Rendement de boite de vitesse

Le rendement d'une boîte de vitesse est estimé comme perdant 2% par couple d'engrenage (correspondant aux frottements entre la roue et le pignon), soit environ 6% de pertes (voir calcul ici) donc un rendement de boite de 94%.

Les pertes dans la transmission sont normalement prises en compte dans les pertes par frottements du véhicule (voir ci-dessous).

Pertes par frottement

La force s'opposant au roulement vient des frottements dans les roulements, dans des frottements de l'interface pneu-route, dans l'échauffement provenant de la déformation du pneu ET de la chaussée à chaque tour de roue, etc. C'est surtout dans la déformation pneumatiques/route qu'est dissipée l'énergie. Les pneus à basse résistance comme les Michelin diminuent de 20% cette résistance au roulement, principalement en reduisant l'écrasement du pneumatique. Comme la déformation de la chaussée intervient aussi, il faut tenir de sur quoi on roule.

F_roul = k.M.g

avec

• F_roul force de résistance au roulement (N)
• k est le coefficient de résistance au roulement, environ 0.012 pour une voiture particulière moderne (0.013 sur le béton ou l'asphalte, 0.015 sur les pavés, 0.02 sur du goudron, 0.05 sur des chemins de terre, 0.1 à 0.35 sur des terres cultivées!), 0.01 pour une méhari avec ses pneus plus étroits et ses roulements à bille de moindre frottement que les roulement coniques imposés par les voitures plus lourdes (0.006 à 0.01 pour des utilitaires à pneus plus rigides sur asphalte). Au passage, une roue de fer sur un rail à un k = 0.001 à 0.002, carrément mieux que le pneumatique, d'où la disparition des michelines et autres métro sur pneus à Paris, malgré le confort supplémentaire accordé (dans les pays où on s'occupe peu de l'énergie comme le canada, on trouve encore des métros sur pneus).
  k est d'autant plus élevé que le rayon de la roue est petit (pas le cas de la méhari, mais des mini par exemple avec leurs roues en 11 pouces) et que le pneu/route se déforme (cas d'un pneu sous gonflé par exemple, la déformation augmentant avec la vitesse (constant jusqu'à 70 km/h, il a augmenté de 10% à 100 km/h), et la masse du véhicule, là encore la méhari à tout bon!).
  Pour résumer, pour la méhari, k vaut 0,01 jusqu'à 70 km/h, puis atteint 0,011 à 100 km/h, nous approximons la montée de façon linéaire, c'est à dire que pour les vitesses supérieures à 70 km/h nous ajoutons à 0,01 la valeur ((vitesse - 70)/30) x 0,001.
• M la masse du véhicule (kg).
• g l'accélération de pesanteur ( 9,81 m/s² ).

Selon la configuration de la méhari, la masse retenue varie de 590 kg ( 530 kg avec un fond de réservoir, pas de bâche et juste 5 kg d'outils et un conducteur de 60 kg, on pourrait même imaginer le cas extrême où le conducteur pousse à côté de la voiture avec un accélérateur à main et en ayant laissé tous les bagages et les portières à terre, ce qui nous ramène à 520 kg) à 1330 kgs (cas avec remorque, PTRA de la méhari). Comme valeur intermédiaire, je prendrais une méhari de 660 kgs (2 personnes légères et 30 kgs de bagages).

Avec sa faible masse, ses pneumatiques de faible largeur (la surface est augmentée par le grand diamètre des roues pour les voitures d'avant 1995, ensuite les roues de 15 pouces sont redevenues la norme) et ses roulement de roue à billes (autorisés par la faible masse à supportée, à partir de 1 T à pleine charge les constructeurs préfèrent utiliser des roulements à rouleau coniques) la méhari est avantagée.

Pertes aérodynamiques

F_aero = 1/2 . ρ . S . Cx . V²

avec

• F_aero force de résistance à la pénétration dans l'air (N)
• ρ la densité volumique de l'air (1,2 kg/m3 au niveau de la mer à 20°C)
• V la vitesse relative du véhicule (tenant compte du vent) en m/s (des km/h divisé par 3,6, par exemple 100 km/h = 27 m/s)
• Cx le coefficient de pénétration dans l'air (0,527 méhari bâchée, 0,475 pare-brise baissé)
• S la surface frontale (2,16 m² avec la bâche, 1,48 m² pare-brise baissé).

Voir p339 du mémento Bosch pour mettre dans la page sur l'éaérodyamique la manière de mesurer la résistance.

Les calculs sur le Cx méhari et la surface frontale ont été estimés dans la page sur l'aérodynamique.

Au niveau aérodynamique, une méhari avec son pare-brise plat et sa grande garde au sol pour le tout terrain sera désavantagée.

Pertes dissipatives en vitesse stabilisée sur le plat

F_ResPlat = F_roul+ F_aero
Les forces de roulement et aérodynamiques seront toujours présentes et toujours dans l'opposition au mouvement. Ces forces sont dissipatives, dans la mesure où on ne pourra jamais les retrouver. L'énergie dissipée est transformée en chaleur.
Dans le cas des essais à vitesse stabilisées sur le plat, il n'y a qu'elles qui s'exercent.

Le cumul de ces 2 forces nous donnera directement la vitesse maxi qu'il est possible d'atteindre en fonction de la force exercée par le moteur. nous verrons cela dans le calcul des puissances.

Les forces que nous allons voir par la suite (gravitation et accélération) ne seront pas forcément toujours un frein à l'avancement, et ne sont plus vraiment des pertes, car leur énergie peut être récupérée dans le cadre d'une regénération électrique par exemple, ou lors d'un mode de fonctionnement inverse (la force de gravité s'opposant au moteur dans la côte sera récupérée dans la descente qui suivra, en aidant le moteur dans son travail).

Gravitation dans les pentes

F_pente = M.g.p%

avec

• F_pente la force s'opposant à l'anvancement dans une côte (force négative dans une descente) (N)
• M la masse du véhicule (kg)
• g l'accélération de la pesanteur ( 9,81 m/s² )
• p% le pourcentage de la pente

Les limites de masse ont déjà été vues pour les forces de frottement.

Les pourcentages mximaux retenus sont 45%, les pentes raides du réseau routier sont de 10%, une pente moyenne est entre 4 et 5%. Le poids du véhicule intervient directement dans les calculs, une voiture légère comme la méhari sera avantagée dans les côtes et sera moins entrainée dans les descentes, usant moins les freins.

Force d'accélération

Toute accélération exerce une force sur la voiture, s'opposant à son avancement. Là encore c'est au moteur à combattre cette force. Il le pourra si les forces d'oppositions vues précédemment ne l'occupent pas à plein temps. Il pourra donc accélérer au démarrage sur le plat. Inutile de lui demander une accélération de fou alors qu'il est dans une côte à 45% avec la caravane au cul.

F_acc= M.γ

avec

• F_acc force s'opposant à l'accélération du véhicule (N)
• M masse (kg)
• γ accélération (m/s²), 1,4 m/s² au démarrage, et jusqu'à -11 m/s² sur un freinage plus ou moins violent.

Les limites de masse ont déjà été vues pour les forces de frottement.

La 2cv6 à une accélération de 0 à 100 km/h en 30 s. Ce qui représente une accélération moyenne de 3,33 km/h /s. Sachant qu'au démarrage, le moteur n'a quasiment aucune autre force à combattre, l'accélération est bien plus vive qu'en approchant des 100 km/h, pratiquement la vitesse maxi de la voiture, où les forces d'opposition sont quasiment aussi fortes que la force maxi que peut fournir le moteur, laissant peu de place à l'accélération.

Suivant des essais d'accélérations que j'avais effectué avec un vieux moteur sans compression (8 bars de compression, segments bloqués en fond de gorge suite à un serrage moteur, faisant lui-même suite à la perte du bouchon de vidange), j'obtenais les temps suivants :

• Passage des vitesses à 25-50-70 km/h (on peut les passer plus haut pour accélérer plus vite).
• 4 s pour aller à 20 km/h
• 10,5 s pour atteindre 50 km/h
• 17 s pour atteindre 60 km/h
• 20 s pour atteindre 65 km/h
• 24,7 s pour atteindre 70 km/h

Soit une accélération passant de 1,39 m/s² à 0,8 m/s² vers 70 km/h (voir le tableur ici), et qui chute encore plus au delà.

Les freinages sont aussi une accélération, mais négative. Il faut en tenir compte dans le cas de la régénération ou dans le dimensionnement des freins (qui dissipent l'énergie en chaleur). D'après un test que j'ai fait, on peut freiner fort mais sans bloquer les roues et avec une bonne marge de 80 km/h à 0 en moins de 3 s (moins de 2,5 s en comptant de tête, c'est pas super précis non plus!). Soit -7 m/s².

Pour un freinage brutal de 1 s pour s'arrêter à 40 km/h (normalement il se fait en encore moins de temps), ça fait -11 m/s² de décélération, soit avec une méhari de 660 kg : F_acc = -7260 N, c'est assez violent pour la voiture, car elle se prends plus de 700 kg poussant vers l'avant. Pour un conducteur de 60 kg, seulement 66 kg, ce qui fait un peu plus d'1 G, ce freinage est loin d'être très violent finalement comparé aux formules 1 où on se prends 2 G dans les virages en latéral.

Sommes des forces s'opposant au roulement

F_ResTot = F_roul+ F_aero+ F_pente+ F_acc

F_penteet F_acc peuvent être négatives si p% et γ le sont (descente ou freinage), c'est à dire que ce sont des forces qui vont avoir tendance à augmenter la vitesse du véhicule dans ces cas-là, et peuvent être récupérées en régénération.

Sans régénération, F_acc ne pourra jamais être récupérée. F_pente pourra l'être s'il ne faut pas freiner dans la descente (en général une bonne descente à pic se termine par un stop... dans ce cas là toute l'énergie est dissipée sous forme de chaleur dans les freins).

On peut remarquer que seul concernant F_aero la méhari sera mauvaise à cause de son SCx (sauf si on baisse le pare-brise) et que dans les 3 autres résistances (roulement, montée et accélération) dépendant du poids, sa faible masse est un avantage non négligeable. D'où l'idée de chercher une utilisation à basse vitesse (ville ou tout terrain) plutôt qu'autoroutière (ou alors en excluant les 6 mois dans l'années où rouler en pare-brise baissé est trop froid, à part s'habiller en motard).

Le moteur doit compenser toutes les forces qui s'exerce contre lui. Il ne peut fournir qu'une force déterminée, assez faible dans le cas de la méhari. Mais nous verrons cette notion de réserve de puissance dans le chapitre sur la puissance.

Couple nécessaire à l'avancement

Cette notion du couple sera détaillée juste pour montrer la notion de couple de démarrage en côte.

Couple de la 2cv

Le couple du flat twin est directement retrouvé à partir des cas extrêmes de fonctionnement rencontrés par le véhicule dans le cadre de son utilisation. Ainsi, le couple doit permettre un démarrage dans une côte à x %.

Retrouvons ce couple par les calculs des couples nécessaire pour combattre les forces d'opposition. Le couple à la roue (couple que l'ensemble moteur-réducteur doit appliquer sur la transmision de la roue) se retrouve avec la force d'opposition F (calculée dans le chapitre précédent des forces d'opposition) et le bras de levier de la roue. Sachant que le rayon d'une roue de 2cv en 15 pouces est de 30 cm (soit r = 0,3 mètre), le couple à la roue est C = F*r = F * 0,3 (en N.m).

Couple de démarrage en côte

Toujours dans le classeur ( ici) nous calculons pour une pente de 45 % et une méhari de 660 kg un couple à exercer sur la roue (que ce soit au démarrage ou en roulant) de C = 873 daN.m.

Pour une méhari de 590 kg avec juste le conducteur C= 780 N.m, et C = 1760 N.m pour une méhari pleine charge avec remorque de 1330 kg.

Difficile d'avoir un moteur aussi coupleux dans une méhari. C'est pourquoi on intercale entre le moteur et la roue une boite de vitesse, dont le rapport total divise d'autant le couple à exercer par le moteur, mais obligeant ce dernier à tourner d'autant plus vite par rapport à la roue.

Sur une 2cv4, le couple DIN en entrée est estimé à 25 N.m à 1500 tr/min, rotation atteinte lors d'un démarrage en côte en faisant patiner l'embrayage. Pour obtenir le couple en sortie de boîte (celui qui s'exerce sur l'axe de la roue, et qui doit contrebalancer celui exercé par le sol sur l'axe de la roue via le pneu et la jante), il suffit de connaitre le rapport de boîte qui donne Ce/Cs = r. Dans la RTA, on trouve r = 0,0348 en première. Ce qui nous donne Cs = 25/0,0348 = 718 Nm. Si je fait patiner l'embrayage au couple max, à 4000 tr/min, j'ai un couple de 28 N.m, ce qui me donne un couple de démarrage à la roue à Cs = 800 N.m.

Sur une 2cv6, le couple DIN en entrée est de 35 N.m à 1500 tr/min, 40 N.m à 4000 tr/min. Le rapport de boîte en première est de 0,0465. Ce qui me donne un couple de démarrage Cs = 752 N.m à 1500 tr/min, et 860 N.m à 4000 tr/min. Une 2cv vide en cirant l'embrayage à 4000 rpm devrait arriver à décoller dans une telle côte. Avec de l'élan à 4000 rpm ça passe de la même façon. Un peu plus lourde, le moteur 602 n'est plus assez puissant, et même avec de l'élan la 2 cv s'arrête en cours de montée.

Pour la méhari, avec une première vitesse de 2cv4 (je ne retrouve plus les valeurs de la méhari d'origine, mais elles sont très proches de la 2cv4) et un moteur 602, ça nous fait un couple à la roue à 1500 rpm de 35 N.m / 0,0348 = 1005 N.m, et 40/0,0348 = 1150 N.m à 4000 rpm. On passe plus facilement les démarrages en côtes, mais le démarrage à pleine charge demandant 1760 N.m reste inaccessible. Seule une méhari de moins de 870 kgs pourra passer une côte de 45 % à 4000 tr/min, et encore pas bien vite.

Au couple absorbé par la pente il faut aussi ajouter le couple de frottement et la résistance aérodynamique, dépendant de la vitesse. C'est pourquoi la 2cv ne pourra pas atteindre sa vitesse max à cause de la force de gravitation s'ajoutant à la résistance de l'air et aux frottements.

Les calculs ne tiennent pas compte du rendement de boite de 94% (pour simplifier les calculs).

Puissance nécessaire à l'avancement

La puissance dissipée est une notion nécessaire pour dimensionner sa voitue en tenant compte des vitesses auxquelles on roule, alors que la notion de couple vue jusqu'à présent ne tient compte que d'une capacité du moteur à franchir un obstacle.

La notion de puissance est indépendante de la présence d'une boite de vitesse ou pas, c'est réellement ce qu'il faut fournir pour combattre les puissances extérieures s'opposant à l'avancement.

La puissance est obtenue en multipliant la force s'opposant à l'avancement (les 4 forces vues précédemment) par la distance sur laquelle s'exerce cette force, ce qui nous donne l'énergie dépensée, puis en divisant par le temps pendant lequel s'exerce cette force, ce qui nous donne la puissance. Comme une distancxe divisée par le temps donne une vitesse, il suffit de multiplier la force déjà vue par la vitesse à laquelle elle s'applique pour obtenir la puissance nécessaire.

Le détail des calculs se trouve dans le tableur Open Office Calc trouvé ici, sur la feuille "résistance avancement".

Puissance de la 2cv

Le calcul de la puissance se fait sur la vitesse maxi, quand toutes les forces d'opposition systématiques (frottement et résistance aérodynamique) sont à leur maximum. La pente et l'accélérations sont des oppositions dépendant du parcours, que l'on ne prends pas en compte pour le calcul de la vitesse maxi, qui se fait sur le plat et sans accélération.
Il faut 22 kW à une méhari bâché pour atteindre 107 km/h, rendement de boite inclus. Cette puissance suffit à combattre les forces s'opposant à l'avancement (frottements divers et résistance de l'air). Gravir une côte augmente la puissance à fournir, il faudra donc diminuer la vitesse (donc les forces aérodynamiques s'opposant à l'avancement) pour gravir la côte, mais ça un deuchiste est au courant!

Puissance dissipée dans les frottements

Soit la formule suivante (voir plus haut pour F_roul) : P_roul =F_roul * V = k.M.g.V

Voyons la courbe en fonction de la vitesse, en faisant varier la masse entre une méhari une seule personne (590 kgs), une méhari moyenne (660 kgs) et une méhari chargée à la toc (1330 kgs):

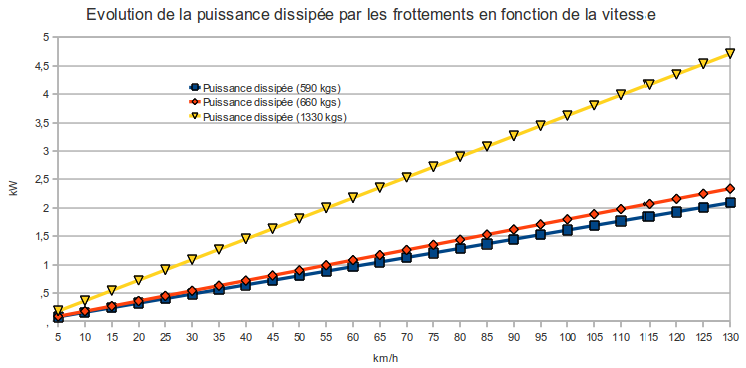
Plus le poids augmente, et plus la puissance consommée est importante, mais ça reste linéaire, et les puissances en jeu restent faibles (moins de 5kW) comparé à l'aérodynamique qui va suivre!

Puissance dissipée en aérodynamique

F_aero = F_aero * V = 1/2 . ρ . S . Cx . V³

C'est la même chose que pour les frottements, on multiplie Faero par la vitesse (la vitesse se retrouve au cube dans l'équation), et on fait varier le facteur du SCx, selon que la méhari soit bâchée ou avec le pare-brise baissé.

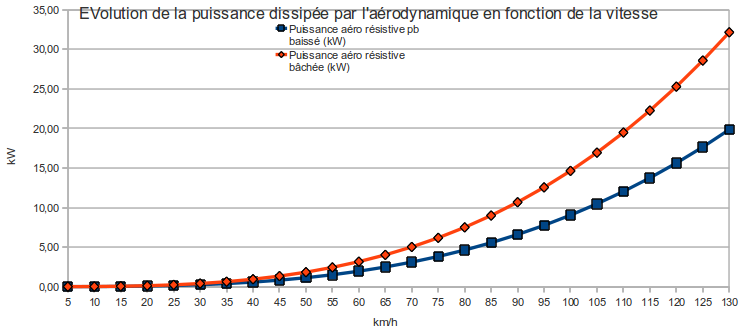
A partir de 70 km/h cette puissance perdue devient significative face aux frottements (on dépasse les 5 kW) et grossit ensuite très vite (l'augmentation est la même entre 0 et 70 km/h qu'entre 70 et 87 km/h, ou entre 120 et 127 km/h, autant dire que les derniers km/h coûtent très chers en énergie!). Cette augmentation s'explique que si la force montait déjà très vite, étant le carré de la vitesse, ici pour la puissance la vitesse est au cube!!!

Pour passer de 90 à 100 km/h, on doit tripler la puissance nécessaire pour aller à 70 km/h. Autant dire que se limiter à 90 km/h n'est pas une mauvaise idée, surtout que le gain de temps entre 90 et 100 est négligeable. Evidemment à 70 km/h (ou 82 km/h pare-brise baissé) on ne consomme quasiment plus rien!

Cet effet est attenué pare-brise baissé.

Puissances dissipatives sur le plat à vitesse constante - vitesse maxi

Prenons les 3 cas suivants : méhari de 660 kg bachée ou pare-brise baissé, et le cas extres méhari avec remorque+bâche.

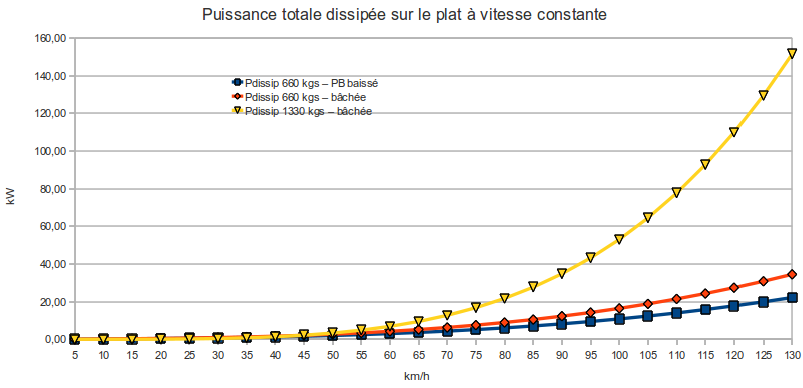
Le cas avec remorque demande trop d'énergie, on saura qu'on ne pourra dépasser les 80 km/h dans ce cas-là. Regardons le cas plus classique hiver-été :

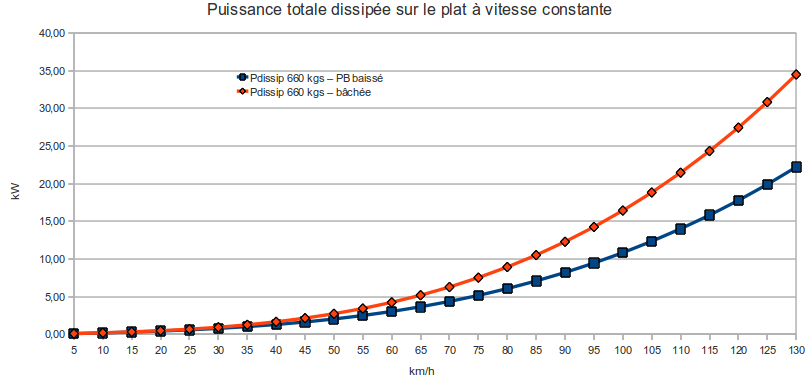
reprendre à partir d'ici

Une méhari de 10 kW sera limitée à 85 km/h bâchée, 100 km/h pare-brise baissé. Il faut 12 kW pour que la méhari bâchée atteigne 90 km/h, ce qui lui fait atteindre 105 km/h pare-brise baissé.

Il faut entre 10 kW (voiture moderne, 3 kW dissipés en frottements et 10 kW en aérodynamique) pour rouler à 100 km/h.

A noter qu'une petite voiture peut rouler à vitesse constante à 100 km/h avec 10 kW. 1 litre d'essence contenant 11 kWh, on pourrait rouler avec un moteur thermique sans pertes  (rendement 100 %) avec 1 l au 100. Les appareils thermiques à meilleurs rendements doivent approcher (dans la théorie) les 50% de rendement, donc on devrait pouvoir parcourir 100 kms à 100 km/h à 2 l aux 100.
La consommation du moteur thermique cesse de décroître vers 60 km/h.

P = F . v
Ainsi, la puissance dissipée à 100 km/h (27m/s) par la force aérodynamique méhari bâchée est de  Paero = F . v = 670 * 27=18 kW, et pare-brise baissé P=280*27=8 kW (d'où l'impression de gagner 10 chevaux (8 kW) en baissant le pare-brise).
Puissance dissipée avec les frottements : P = Froul.v = 65*27 = 1,8 kW
A comparer aux chiffres pour une petite voiture moderne, 7kW dissipé en aérodynamique et 3 kW dissipés en roulement.
Mais avec un moteur électrique, il est possible d'abaisser le capot de la méhari, de réduire la calandre (beaucoup moins de refroidissement) et donc de gagner en Cx, sans compter l'installation d'un hard-top profilé, et surtout un pare-brise bombé (tant qu'à faire qu'à homologuer un moteur électrique...).
Ainsi, en roulant à 100 km/h en vitesse stabilisée, la puissance absorbée sera de 20 kW avec la bâche, et 10 kW sans la bâche. On retombe un peu sur la bonne moyenne de 15 kW maxi.

Pour des vitesses urbaines inférieures à 50 km/h (13 m/s) bâchée : Paero = 0,6*1,54*13exp3 = 2 kW, soit autant que pour les roulements. Pare-brise baissé, Paero =  0,6*0,7*13exp3 = 0,9 kW

A ces vitesses là, les forces s'opposant à l'avancement sont surtout dépendantes du poids. Au dessus, c'est le Cx qui prime.

A 50 km/h, à vitesse stabilisée, la méhari consomme une puissance de 3 kW (1 kW aero pb baissé+2 kW roul) chaque seconde, et donc une énergie pendant une heure de 3 000*3 600 = 10 800 000 J pour 50 km, et donc 10 800 000/50 = 216 000 J/km soit 216 000/3600 = 60 Wh/km. La méhari étant estimée à 650 kgs pour les calculs, nous avons 60/650 = 0,09 Wh/km/kg.
On donne une conso moyenne de puissance à 50 km/h de 0,050 à 0,200 Wh/km/kg en fonction du véhicule, la méhari est donc dans la fourchette basse grâce au pare-brise baissé.

On sait que quoiqu'il arrive à 50 km/h la méhari consommera 60 Wh/km (pour info, un vélo électrique c'est 7 Wh/km, plus léger, moins rapide et avec la moitié de l'énergie fournie sous forme musculaire). Après, il faut avoir un bon rendement total pour ne pas s'éloigner de cette conso théorique, les pertes diverses font monter la facture.

On s'aperçoit en effet qu'avec les rendements de charge, le rendement moteur, etc, on arrive plutôt à des consos entre 15 et 25 Wh/km. Après, la récupération d'énergie permet de tomber à des valeurs très faibles comme les 100 Wh/km de la dyane Donnier.

Calculons la conso de la méhari à 100 km/h : Puissance consommée de 12 kW sans la bâche, soit 12 000 / 100 = 120 Wh/km. Avec la bâche, ça donne 20 kW soit 200 Wh/km. Voilà une des raisons pourquoi pare-brise levé je ne dépasse pas 80 km/h...

Puissance dissipée en pente

Cette puissance vient s'ajouter à celle nécessaire au roulement sur le plat. Si la puissance du moteur reste identique (pédale d'accélérateur inchangée) la vitesse augmente si on descend (puissance négative, ou plutôt apportée à la roue par le poids du véhicule) et la vitesse diminue si on monte. Pour ne pas voir baisser la vitesse, il faut accélérer pour augmenter la puissance du moteur ... s'il en reste. Si on roule en méhari bâchée à 107 km/h, on utilise toute la puissance du moteur pour battre la réistance de roulement et d'avancement à l'air, il n'y a plus rien pour contrebalancer l'opposition faite par la gravité au changement d'altitude de la voiture. La vitesse chute.

Pour gravir une pente de 45 % (histoire de pouvoir jouer un peu en 4x4), la force qui s'oppose à la méhari de 650 kg est de :
Fpente = Mgp% = 650*9,8*0,45 = 6370*0,45 = 2 850 N
Soit une puissance dissipée de Ppente=Fpente*V = 37 kW à 50 km/h (13m/s), et 8,6 kW à 11km/h (3 m/s). Avec 10 kW de puissance on passe à 10 km/h avec la résistance au roulement.
Les côtes habituellement rencontrées sont maxi de 15%, il faut pouvoir les franchir à au moins 50 km/h (13m/s), soit Ppente = 6370*0,15*13 = 12,5 kW. Mouais, c'est pas gagné là, on ne passe plus avec les 4 kW de frottement en plus! A moins d'avoir 18 kW.
Une pente de 10 % devrait être gravie à au moins 60 km/h (17m/s), soit Ppente = 6370*0,1*17 = 11 kW. Là encore, on passe avec le 18 kW, mais à 15 kW on n'est pas très loin non plus, et c'est pas quelques km/h en moins (surtout aux alentours de 60 km/h) qui vont changer grand chose à l'heure d'arrivée.
Et l'avantage de la méhari, c'est que les gens derrière savent que la voiture est à fond, donc pardonnent plus facilement!

Là encore, la méhari a besoin de peu de puissance grâce à son faible poids.

Tant qu'on y est avec la pente, calculons maintenant l'effort maximal à fournir.
La force pour décoller la voiture dans une pente de 60% (là ça commence à être du costaud) est de Fpente = 6370 * 0.6 = 3 800 N. Si on veut se limiter aux meilleurs 4x4, on reste à 45 % soit 2 900 N

Puissance dissipée à l'accélération

Pour l'instant nous zappons cette histoire d'accélération, elle sera lamentable si la méhari est à haute vitesse en montée. Sinon, elle sera directement dépendante de la puissance maxi non utilisée. Sachant qu'il vaut mieux accélérer lentement pour l'autonomie.

Puissance dépensée pendant un cycle de conduite

Lorsqu'on conduit, on accélère, freine, on monte, on descend. les cycles normalisés reproduisent ces conditions. Le lien suivant :

http://www.hkw-aero.fr/pdf/energie_utile_voiture.pdf

Montre que dans un cycle européen standard, c'est surtout la masse du véhicule qui bouffe l'énergie sans regénération, et est à égalité avec l'aérodynamisme si je récupère l'énergie au freinage.

37% de l'énergie dépensée pour un cycle européen (censé être représentatif d'un fonctionnement moyen des automobiles) vient de l'accélération (stockage de l'énergie dans l'énergie cinétique) d'où l'intérêt de la régénération au freinage.

Résumé

Puissance

Une puissance est une force multiplié par la vitesse, ou une énergie dérivée par rapport au temps, ou un couple multiplié par une vitesse angulaire.
P = C.ω = dE/dt = F.v
avec:

P la puissance en W (Watts), encore exprimé en J/s (Joules par seconde), ou en N.m/s² (Newtons.mètres par seconde carrée).
C le couple en N.m
ω en radian/s
E l'énergie en Joules
F une force en Newton
v une vitesse en m/s.

La puissance peut être vue comme un débit d'énergie.

La puissance d'un moteur correspond à la puissance maximale que l'on peut tirer du moteur, accélérateur grand ouvert.

Cette puissance peut être augmentée en donnant plus souvent de petites impulsions d'énergie (on monte dans les tours), ou en donnant de plus importantes impulsions d'énergie (on augmente la quantité de mélange admis, on augmente l'énergie issue de l'explosion (par exemple par enrichissement du mélange)).

à suivre...