Nouvelle Normalisation
Angles en base 6

Sommaire de la page

---

Préambule

Comme toutes les pages en base 6, je prends la convention suivante : Les chiffres arabes (1, 2, 3, 4, 5, 6, 7, 8, 9) indiquent une base 10 et une norme SI. Les chiffres en base 6 sont notées avec les majuscules suivantes : D=1, F=2, J=3, K=4, L=5, D0=10₆ (6₁₀), DD=11₆ (7₁₀), etc. Le zéro 0 reste le même dans toutes les bases !

Au lieu de diviser le tour en 360°, ce qui est compliqué pour les calculs, on va le décomposer en K0° (24°). Ce qui permet d'avoir les angles de l'horloges analogique, plus les angles à 45° (angle droit divisé par 2). Ensuite, c'est les décimales qui s'occuperont des calculs précis si on en a besoin, la plupart du temps les angles de 120°, 90°, 60°, 45°, 30° suffisent.

Pourquoi avoir choisi 360° ?

Personne n'en sait rien, mais il y a fort à parier qu'il s'agisse de croyances en la numérologie annunaki des Sumériens. Reprenons cette analyse mathématique trouvée sur la page wikipédia concernant le degré :

Les sumériens ont imposé leur système de notation aux civilisations ultérieures qu'ils ont fondé partout dans le monde. Les sumériens avaient une base sexagésimale (le paquet ne vaut pas 6 comme en sénaire, ou 10 comme en décimal, mais 60 (DK0).

La figure géométrique la plus simple qui soit n'est pas le cercle, mais le triangle équilatéral, avec ses trois côtés et ses trois angles égaux. Il semble plus logique et plus cohérent de penser que les Sumériens, pour définir le degré d'angle, aient pris l'angle du triangle équilatéral comme référence et qu'ils l'ont, en application de leur base sexagésimale, divisé en 60 degrés, puis le degré en 60 minutes d'angle, puis la minute en 60 secondes d'angle.

La somme des 3 angles d'un triangle étant égale à un angle plat (2 angles droits). L'angle plat devant être un multiple de 3 (3 angles triangle), il a été choisi 60×3=180 degrés. L'angle droit (la moitié de l'angle plat) vaut 90 degrés. Le tour complet, qui vaut deux angles plats, vaut donc 360 degrés (6 en base 60, proche de 2 fois pi et donc des radians, qui sont une base dont l'unité est pi =3.141516).

En résumé, le degré serait plutôt, par définition, la 60ème partie d'un angle de triangle équilatéral (angle de référence).

angles retenus : cercle = K0°

Si on regarde les angles courants, il nous faut l'angle plat p (180°), l'angle droit (p/2; 90°), l'angle plat divisé par 3 (p/3, 60°), l'angle droit divisé par 2 (p/2/2 = p/4, 45°), l'angle droit divisé par 3 (p/2/3 = p/6, 30°). Ensuite, il est difficile à l'oeil humain de décomposer plus un quadrant de cercle (exemple, une horloge) sans se tromper au premier coup d'oeil. on passera ensuite au chiffre sous la virgule pour détailler.

Pour que ces angles courants soient exprimés de façon entière, en base 6, sachant qu'il nous faut l'angle p/4, 4 n'étant pas un diviseur de D0 mais de F0, il nous faut retenir F0 pour l'angle plat. L'unité d'angle sera donc p/F0 (p/12 = 15°).

Le cercle vaut donc K0°, l'angle plat 2p/3 = F0°, l'angle droit p/2 = D0°, p/3 = K°, p/4 = J°, p/10 = F° et p/20 = D°.

La somme des angles du triangle font F0°, le triangle équilatéral ayant des angles identiques de K°.

Comparaison des angles entre les degrés adam et les degrés sexa :

degré sexa (base 10)	degré adam (base 6)
360	K0
180	F0
120	DF
90	D0
60	K
45	J
30	F
15	D

Les angles principaux sont plus simples. Dans l'image suivante :

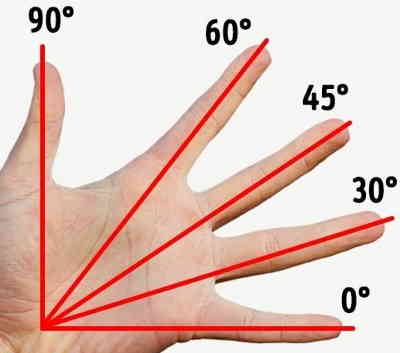
On a, en partant du bas, F au lieu de 30, J au lieu de 45, K au lieu de 60, D0 au lieu de 90.

à suivre...